Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 19
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto no Problema 1. 18.
Passo 1
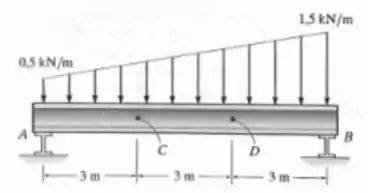
Faalaa, tá bem? Bora lá! Primeiro passo nesse tipo de questão é achar as reações nos apoios dos pontos e .
Para isso, a gente precisa achar forças concentradas equivalentes a esse carregamento distribuído, tá bem? Ele tem a cara de um trapézio, então a gente pode dividir esse carregamento em um retângulo e um triângulo, assim:
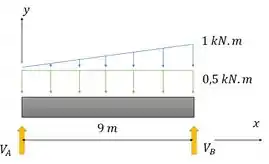
Da carga em formato de retângulo, a força concentrada resultante vai ser a área do retângulo:
E o ponto de ação dela vai ser na linha que passa pelo centroide desse retângulo, ou seja, na metade dele, em .
A força resultante para a carga em formato de triângulo também vai ter o valor da área do triângulo
E o ponto de ação dela também está na linha que passa pelo centroide do triângulo. Ele está localizado a dois terços da ponta do triângulo, então nossa força está em
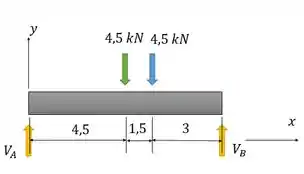
Logo, nosso DCL fica:
Passo 2
Agora nós utilizaremos as equações de equilíbrio de forças e momentos para achar e . Vamos considerar que o sentido positivo do momento é o anti-horário e vamos calcular o momento no ponto , pois assim sumimos com o .
E então calcularemos as forças na vertical para encontrar :
Uhul! Achamos os valores dos apoios!
Passo 3
Aí nossa esqueminha fica assim:
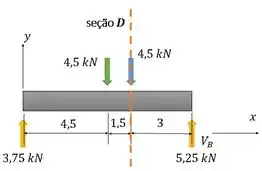
Mas, para achar os esforços aplicados na nossa seção , precisamos voltar aquela carinha de cargas distribuídas:
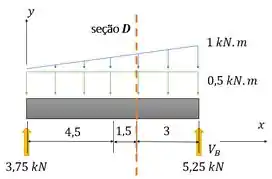
Aí vem uma parte divertida: a gente pode simplesmente escolher um dos lados da nossa viga em relação a seção e descartar o outro. Eu vou escolher o lado da esquerda, porque o lado da direita tem uma carga em forma de trapézio, ruinzinha de trabalhar.
E aí no lugar do pedaço da viga que estava ali, a gente coloca icógnitas representando os esforços internos que passam por essa seção e a gente quer descobrir, assim:
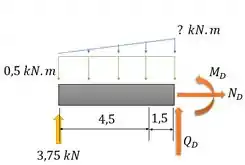
Passo 4
Fofo, né? Mas repara que a gente não sabe o valor da altura do triângulo azul, isso porque a gente cortou o triângulo maior de altura 1, lembra? A gente precisa descobrir essa altura aí. Vamos usar semelhança de triângulos.
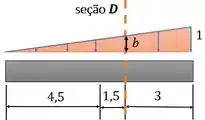
Daí:
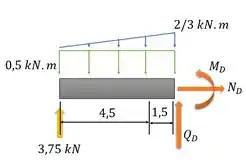
E calculando as forças concentradas equivalentes a essas cargas distribuídas, assim como a gente fez no passo 1, com a força sendo igual ao valor da área da carga e sua localização passando pelo centroide dessa área, temos:
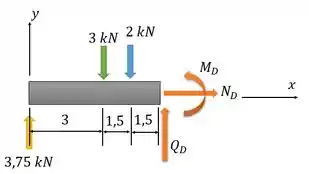
Passo 5
Agora a gente usa as equações de equilíbrio para achar esses esforços internos e :
Comparando esses valores que a gente achou para o caso convencionado como positivo (quando a gente fica só com a parte da esquerda da nossa seção):
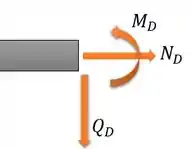
A gente vê que o nosso cortante está no sinal contrário. Então, na real, nossos esforços ficam:
(Obs.: No capítulo 1 do Hibbeler, ainda não foi mencionado a convenção para a direção dos esforços internos e por isso que o valor encontrado aqui foi negativo.)