Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 113

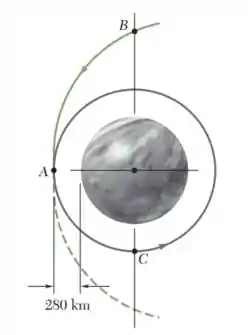
Determine o tempo necessário para uma sonda espacial do Problema 12.99 viajar de B para C.

Passo 1

Para solução do Problema 12.99, nós temos

( v A ) p a r = 10,131.4   m / s

e

( v A ) c i r = 1 2 ( v A ) p a r = 7164.0   m / s

Também,

r A = 6052 + 280 k m = 6332   k m

Para a tragetório parabolica BA, nós temos

1 r = G M v h B A 2 ( 1 + ε   c o s θ )       [ E q . 12.39 ' ]

Onde ε = 1 . Agora

Para A, θ = 0 :

1 r A = G M v h B A 2 ( 1 + 1 )  

ou

r A = h B A 2 2 G M V

Para B, θ = - 90 º :

1 r B = G M v h B A 2 ( 1 + 0 )

r B = h B A 2 G M V

Ou

r B = 2 r A

Passo 2

Como a sonda viaja de B para A, a área percorrida é a área semi parabolica definida pelo Vertex A e Ponto B, Então,

( Á r e a   p e r c o r r i d a ) B A = A B A = 2 3 r A r B = 4 3 r A 2

Agora

d A d t = 1 2 h

Onde h = constante

Então

A = 1 2 h t       o u       t B A = 2 A B A h B A       h B A = r A v A = 2 x 4 3 r A 2 r A v A = 8 3 r A v A

                                                            = 8 3 6332 × 10 3 m 10,131.4   m / s = 1666.63   s

Passo 3

Para a tagetória circular AC,

T A C = π 2 r A ( v A ) c i r c = π 2 6332 × 10 3 7164.0   m / s = 1388.37   s

Passo 4

Finalmente,

T B C =   T B A + T A C

= 1666.63 + 1388.37 s = 3055.0   s

ou T B C = 50 min ⁡ 55   s  

Resposta

T B C = 50 min ⁡ 55   s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade escalar constante máxima que um carro de corrida pode ter se a aceleração do carro não pode exceder 7,5m / s 2 enquanto gira em uma pista tendo um raio de curvatura de 200m .
Um carro viaja ao longo de uma pista circular de raio 75m , e sua velocidade escalar por curto período de tempo 0 ≤ t ≤ 2s e v = 0,9 t + t 2m / s , onde t é dado em segundos. Determine a intensidade d
O barco move-se ao longo de uma linha reta com a velocidade escalar descrita pelo gráfico. Construa os gráficos s - t e a - s . Determine também o tempo necessário para o barco se deslocar a distancia
O anel de 2,5 kg desliza sobre a barra lisa, de maneira que quando ele está em A ele tem velocidade de 3 m/s. Se a mola à qual ele está ligado tem comprimento não deformado de 0,9 m e rigidez de k = 1
Uma partícula de 2 kg desloca-se ao longo de uma trajetória lisa horizontal definida por r = 1 4 t 3 + 2m , θ = t 2 4r a d Onde t é dado em segundos. Determine as componentes da força radial e transve