Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas de Revisão - Ex. 71

r . Determine a tensão de cisalhamento máxima produzida pelas duas forças iguais e opostas P   e   P ' . Sugestão: primeiramente, determine a força cortante V e o torque T em uma seção transversal.)

Passo 1

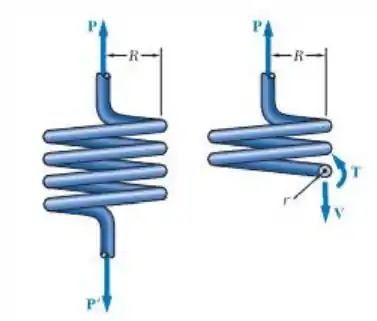
E ai gurizada tudo bem? O enunciado pede que a gente determine a força cortante V e o torque T em uma seção transversal.)

Então consideramos que:

+ ↑ Σ F y = 0 :                     P - V = 0               V = P

+ ↺ Σ M c = 0 :                   T - P R = 0           T = P R

Passo 2

A tensão de cisalhamento por T é dada como:

τ r = T C J = 2 T π c 3 = 2 P R π r 3

Tensão cisalhamento por V.

Para um semicírculo,

Q = 2 3 r 3 ,   t = d = 2 r

Para uma seção circular sólida

I = 1 2 J = π 4 r 3

τ v = V Q I t = V 2 3 r 3 π 4 r 4 2 r = 4 V 3 π r 2 = 4 P / 3 π r 2

Por superposição,

τ m a x = τ T + τ v                                                 τ m a x = P 2 R + 4 r 3 π r 3

Resposta

τ m a x = P 2 R + 4 r 3 π r 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo de aço AB tem 100MM de diâmetro externo e parede com 8mm de espessura. Sabendo que a tensão no cabo é de 40kN, determine as tensões normal e de cisalhamento no ponto H.
Duas forças são aplicadas ao tubo AB, conforme mostra a figura. Sabendo que o tubo tem diâmetros interno e externo iguais a 35mm e 42 mm, respectivamente, determine as tensões normal e de cisalhamento
O tubo de aço AB tem um diâmetro externo de 72mm e uma parede de 5 mm de espessura. Sabendo que o braço CDE está fixado rigidamente ao tubo, determine as tensões principais, os planos principais e a t
Várias forças são aplicadas ao tubo montado conforme a figura. Sabendo que o tubo tem diâmetros interno e externo iguais a 40,9mm e 48,3mm, respectivamente, determine as tensões normal e de cisalhamen
Três forças são aplicadas à barra mostrada na figura. Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.