Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 42

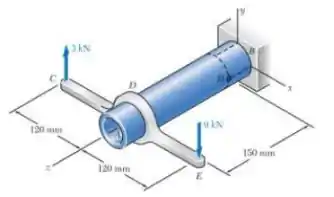
O tubo de aço AB tem um diâmetro externo de 72mm e uma parede de 5 mm de espessura. Sabendo que o braço CDE está fixado rigidamente ao tubo, determine as tensões principais, os planos principais e a tensão de cisalhamento máxima no ponto H.

Passo 1

E ai gurizada vamos começar substituindo as forças em C e E por uma equivalente no sistema D. Consideramos o esboço abaixo :D

F D = 9 - 3 = 6 k N ↓

T D = 9 x 10 3 120 x 10 - 3 + 3 x 10 3 120 x 10 - 3 = 1440 N   ∙ m

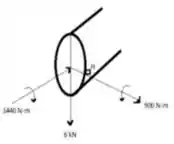
Na seção contendo o ponto H:

P = 0       V = 6 k N       T = 1440 N ∙ m

M = ( 6 x 10 3 150 x 10 - 3 = 900 N ∙ m

Passo 2

Propriedades da seção:

d 0 = 72 m m   c o = 1 2 d o = 36 m m   c i = c o - t = 31 m m

Determinando a área temos:

A = π c o 2 - c i 2 = 1,0524 x 10 3 m m 2 = 1,0524 x 10 - 3 m 2

I = π 4 c o 4 - c i 4 = 593,84 x 10 - 3 m m 4 = 593,84 x 10 - 9 m 4

J = 2 I = 1,1877 x 10 - 6 m 4

Passo 3

Para meio cano:

Q = 2 3 c o 3 - c i 3 = 11,243 x 10 3 m m 3 = 11,243 x 10 - 6 m 3

No ponto H: ponto H está no eixo neutro de dobra. σ H = 0  

τ H = T c J + V Q I t = 1440 36 x 10 - 3 1,1877 x 10 - 6 + 6 x 10 3 11,243 x 10 - 6 593,84 x 10 - 9 10 x 10 3 = 55,0   M P a

Passo 4

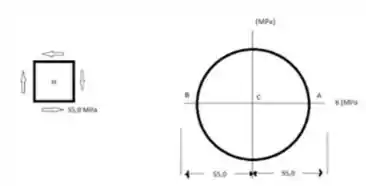
Usando círculo de Mohr. σ c = 0  

R = 55,0 M P a

σ a = σ c + R                                                 σ a = 55,0 M P a

σ b = σ c - R                                          

σ b = - 55,0 M P a

θ a = - 45 ° , θ b = + 45 °

τ M A X = R                                                                

τ M A X = 55,0 M P a

Resposta

55,0 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força P centrada é aplicada a um pilar curto conforme mostrado. Sabendo que as tensões no plano a - a são σ = - 15k s i e τ = 5k s i , determine (a) o ânguloβ que o plano a - a forma com a horizonta
Um mecânico usa um pé de cabra para soltar um parafuso em E . Sabendo que o mecânico aplica uma força vertical de 24l b em A , determine as tensões principais e a máxima tensão de cisalhamento no pont
Um tubo de aço A B tem 102m m de diâmetro externo e espessura da parede de 6m m . Sabendo que o braço C D é rigidamente conectado ao tubo, determine as tensões principais e a tensão máxima de cisalham
Duas forças de 5,34k N são aplicadas a um elemento de máquina AB em forma de L, conforme mostrada a figura. Determine as tensões normal e de cisalhamentos (a) no ponto a ,(b)no ponto b ,(c)no ponto c.
Duas forças de 5,34k N são aplicadas a um elemento de máquina AB em forma de L,conforme mostrada a figura.Determine as tensões normal e de cisalhamentos (a) no ponto d,(b)no ponto e ,(c)no ponto f.