Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 38

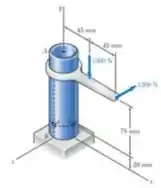
Duas forças são aplicadas ao tubo AB, conforme mostra a figura. Sabendo que o tubo tem diâmetros interno e externo iguais a 35mm e 42 mm, respectivamente, determine as tensões normal e de cisalhamento (a) no ponto a e (b) no ponto b.

Passo 1

E ai gurizada tudo certo? O enunciado pede que a gente determine as tensões normal e de cisalhamento (a) no ponto a e (b) no ponto b. Vamos considerar o esboço abaixo :D

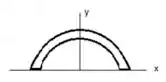
Temos então que determinar a área a partir do centroide vem comigo :D

C o = d o 2 = 21 m m ,         C i = d i 2 = 17,5 m m          

A = π c 0 2 - c i 2 = 423,33 m m 2

Então vamos determinar a inércia ;)

J = π 2 c 0 4 - c i 4 = 158,166 x 10 3 m m 4             I = 1 2 J = 79,083 x 10 3 m m 4

Passo 2

Para um semicírculo com um corte externo semicircular:

Q = 2 3 c 0 3 - C i 3 = 2,6011 x 10 3 m m 3

Na seção contando pontos a e b:

P = - 1500 N           V z = - 1200 N       V x = 0

Podemos determinar o momento em x e z e depois o torque ;)

M z = - 45 x 10 - 3 1500 = 67,5 N . m

M x = - 75 x 10 - 3 1200 = - 90 N . m

T = 90 x 10 - 3 1200 = 108 N . m

Passo 3

Agora podemos determinar as tensões normal e de cisalhamento (a) no ponto a:

σ = P A - M x c I = - 1500 423,33 x 10 - 6 - - 90 21 x 10 - 3 79,083 x 10 - 9 = 20,4 M P a

τ = T c J + V x Q I t = 108 21 x 10 - 3 158,166 x 10 - 9 + 0   = 14,34 M P a

Passo 4

Agora podemos determinar as tensões normal e de cisalhamento (b) no ponto b:

σ = P A + M z c I = - 1500 423 x 33 x 10 - 6 + - 67,5 21 x 10 - 3 79 x 083 x 10 - 9                                            

  σ = - 21,5 M P a

τ = T c J + V 2 Q I t = 108 21 x 10 - 3 158,166 x 10 - 9 + 1200 2,6011 x 10 - 6 79,083 x 10 - 9 7 x 10 - 3                        

τ = 19,98 M p a            

Resposta

  1. 20,4 M P a   e   14,34 M P a  
  2. - 21,5 M P a   e   19,98 M p a            
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o estado de tensão no ponto B quando a viga está sujeita à força de 4 kN no cabo. Indique o resultado como um elemento de volume diferencial.
Dois elementos de madeira de seção transversal retangular uniforme de 80 × 120m m são unidos por uma junta colada conforme mostra a figura. Sabendo que β = 22 ° e que as tensões máximas admissíveis na
Dois elementos de seção transversal uniforme de 50 m m × 80 m m são colados entre si ao longo do plano a - a , que forma um ângulo de 25 ° com a horizontal. Sabendo que as tensões admissíveis para a j
O eixo de um automóvel está sob a ação das forças e torque mostrados na figura. Sabendo que o diâmetro do eixo de seção transversal cheia é de 32 m m , determine (a) os planos e tensões principais no
Uma força vertical de 400l b é aplicada em D em uma engrenagem fixada ao eixo sólido A B de 1i n de diâmetro. Determine as tensões principais e a tensão de cisalhamento máxima no ponto H localizado no