Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 40
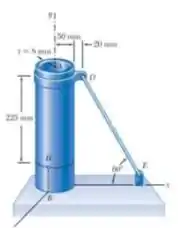
O tubo de aço AB tem 100MM de diâmetro externo e parede com 8mm de espessura. Sabendo que a tensão no cabo é de 40kN, determine as tensões normal e de cisalhamento no ponto H.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine as tensões normal e de cisalhamento no ponto H, vamos começar calculando as forças verticais e horizontais.
Força vertical:
Força Horizontal:
Ponto H no eixo neutro de dobra.
Passo 2
Agora iremos determinar as propriedades da seção:
Calculando a área temos:
Para o cano fino:
Resposta
Exercícios de Livros Relacionados
Um poste com as dimensões mostradas na figura está sujeito à carga de apoio P. Especifique a região na qual essa carga pode ser aplicada sem provocar o desenvolvimento de tensão de tração nos pontos A
A pilastra de alvenaria está sujeita à carga de 800 kN. Se x = 0,25 m e y = 0,5 m, determine a tensão normal em cada canto A, B, C, D (não mostrado na figura) e trace a distribuição da tensão na seção
A haste maciça de 25 mm de diâmetro está sujeita às cargas mostradas na figura. Determine o estado de tensão no ponto A e mostre os resultados em um elemento diferencial localizado nesse ponto
O homem tem massa de 100 kg e centro de massa em G. Se ele mantiver na posição mostrada na figura, determine a tensão de tração máxima e a tensão de compressão máxima desenvolvida na seção a-a da barr
Determine o estado de tensão no ponto A quando a viga está sujeita à força de 4 kN no cabo. Indique o resultado como um elemento de volume diferencial.