Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 45

Três forças são aplicadas à barra mostrada na figura. Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.

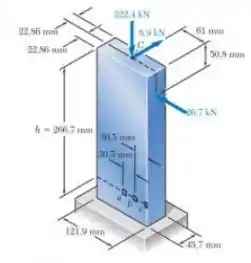
Passo 1

Calcule as forças e momentos na seção considerando os pontos a, b, e c., com base no esboço a seguir:

h = 266,7   m m .

P = 222,4   k N ;     V x = 26,7   k N ,       V z = 8,9   k N  

M z = 266,7 - 50,8 26,7 = 5764,53   k N ⋅ m m

M x = 266,7 8,9 = 2373,63   k N ⋅ m m

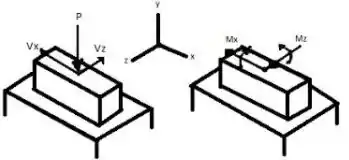
Propriedades da seção:

A = 121,9 45,72 = 5573,3   m m 2

I x = 1 12 121,9 45,72 3 = 970825   m m 4

I z = 1 12 45,72 121,9 3 = 6901382   m m 4

Passo 2

A tensão é dada por:

σ = - P A + M z x I z + M x z I x           τ = V x Q I z t

Vamos começar então aplicando essas fórmulas para o item (a)

Ponto a: x = 0 ,     z = 22,86   m m ,    

Q = 45,72 61 30,5 = 85062,06   m m 3

σ = - 222,4 * 10 3 5573,3 + 0 + 2373,63 * 10 6 22,86 970825

σ = 15,99   M P a

τ = 26,7 * 10 3 85062,06 6901382 45,72

τ = 7,2   M P a

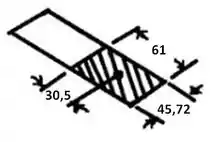
Passo 3

Fazendo o mesmo para o item (b)

Ponto b: x = 30,5   m m ,     z = 22,86   m m

Q = 45,72 30,5 45,75 = 63838,41   m m 3

σ = - 222,4 * 10 3 5573,3 + 5764,53 * 10 3 30,5 6901382 + 2373,63 * 10 3 22,86 970825

σ = 41,46   M P a

τ = 26,7 * 10 3 63838,41 6901382 45,72

τ = 5,72   M P a

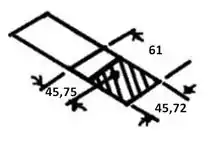
Passo 4

E, finalmente, para o item (c)

Ponto c: x = 61   m m ,     z = 22,86   m m ,       Q = 0  

σ = - 222,4 * 10 3 5573,3 + 5764,53 * 10 3 61 6901382 + 2373,63 * 10 3 22,86 970825

σ = 66,94   M P a

τ = 0

Resposta

(a)

σ = 15,99   M P a

τ = 7,2   M P a

(b)

σ = 41,46   M P a

τ = 5,72   M P a

(c)

σ = 66,94   M P a

τ = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força de 13kN é aplicada a coluna ABD com 60mm de diâmetro de ferro fundido conforme mostrado. No ponto H, determine (a) as tensões principais e os planos principais, (b) a tensão de cisalhamento
Três forças são aplicadas a uma placa com 101,6mm de diâmetro que está fixada a um eixo cheio AB de 45,7 mm de diâmetro. No ponto H, determine (a) as tensões e os planos principais e (b) a tensão de c
O tubo de aço AB tem 100MM de diâmetro externo e parede com 8mm de espessura. Sabendo que a tensão no cabo é de 40kN, determine as tensões normal e de cisalhamento no ponto H.
Duas forças são aplicadas ao tubo AB, conforme mostra a figura. Sabendo que o tubo tem diâmetros interno e externo iguais a 35mm e 42 mm, respectivamente, determine as tensões normal e de cisalhamento
O tubo de aço AB tem um diâmetro externo de 72mm e uma parede de 5 mm de espessura. Sabendo que o braço CDE está fixado rigidamente ao tubo, determine as tensões principais, os planos principais e a t