Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 39

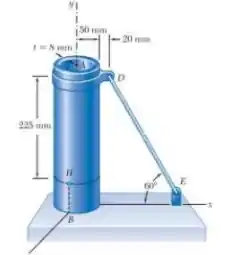
Várias forças são aplicadas ao tubo montado conforme a figura. Sabendo que o tubo tem diâmetros interno e externo iguais a 40,9mm e 48,3mm, respectivamente, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K. Considere o esboço abaixo :D

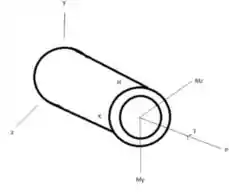
Propriedades da seção:

P = 150 l b

T = 200 l b 10 i n . = 2000 l b   .     i n .

Determinando os momentos em y e z temos:

M z = 150 l b 10 i n . = 1500 l b   .     i n .

M y = 200 l b - 50 l b 10 i n . - 150 l b 4 i n . = 900 l b   .     i n .

V z = 2000 - 150 - 50 = 0

V y = 0

Passo 2

Agora vamos determinar a área e a inércia consequentemente temos:

A = π 0,95 2 - 0,805 2 = 0,79946 i n 2

I = π 4 0,95 4 - 0,805 4 = 0,30989   i n 4

J = 2 I = 0,61979 i n 4

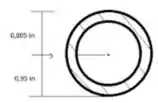
Passo 3

Ponto H: σ H = P A + M z c I = 150 l b 0,79946 i n 2 + 1500 l b   .     i n . 0,95 i n . 0,30989 i n 4 = 187,6 p s i + 4593 p s i σ H = 4,79 k s i

τ H = T c J = 2000 l b   .     i n . 095 i n . 061979 i n 4 = 3065,6 p s i

τ H = 3,07 k s i

Passo 4

Ponto K: σ K = P A + M y c I = 150 l b 0,79946 i n 2 - 900 l b     .     i n . 0,95   i n . 0,30989 i n 4 = 187,6 p s i - 2759 p s i          

σ K = - 2,57 k s i

τ K = T c J =   τ H                                                  

τ K = 3,07 k s i

Resposta

  1. 4,79 k s i   e   3,07 k s i  
  2. - 2,57 k s i   e   3,07 k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força de 10kN e um momento de 1,4 k N ∙ m são aplicados na extremidade livre de uma barra de ferro fundido de 65mm de diâmetro, mostrada na figura. Determine as tensões normal e de cisalhamento (a
A viga em balanço AB tem uma seção transversal retangular de 150m m×200m m . Sabendo que a força de tração no cabo BD é de 10,40k N e desprezando o peso da viga ,determine as tensões normal e de cisal
A componente AB tem uma seção transversal retangular uniforme de 10×24m m . Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.
A componente AB tem uma seção transversal retangular uniforme de 10mm x 24mm. Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.
A componente AB tem uma seção transversal retangular uniforme de 10×24m m . Para o carregamento mostrado, determine as tensões normal e de cisalhamento (a) no ponto H e (b) no ponto K.