Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 72
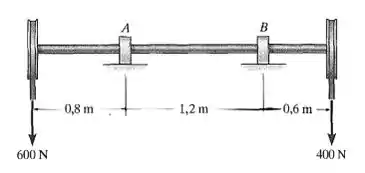
Determine a tensão de flexão máxima absoluta no eixo de de diâmetro que está sujeito às forças concentradas. Os mancais de luva em e suportam somente forças verticais.
Passo 1
Fala aí pessoal, partiu mais um problema de resmat. Ele pediu a tensão de flexão máxima absoluta nesse cara. Então a gente precisa achar nele o momento máximo e usar a fórmulinha da flexão para a tensão. Bora!
Primeiramente, a gente vai começar observando as propriedades geométricas dessa seção.
Vamos começar pelo momento de inérciaele será dado por:
Onde é o raio do nosso eixo.
É isso. Vamos seguir!
Passo 2
Aí a gente quer o momento máximo nessa viga para achar a tensão máxima. Precisamos para isso do diagrama de momento.
Primeiro se acha as reações de apoio:
Passo 3
Como só temos cargas pontuais e nenhum momento concentrado, a gente pode calcular só os momentos nos apoios e marcar eles no diagrama. Os momentos nas extremidades serão nulos.
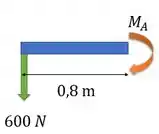
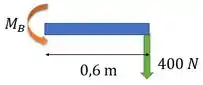
Podemos então fazer o diagrama:
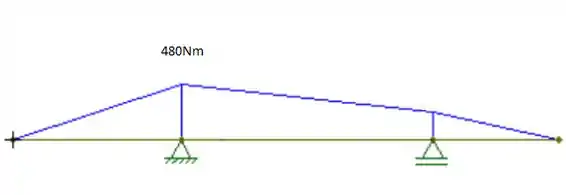
Passo 4
Temos tudo agora para montar a fórmulinha da tensão:
Podemos ver que o momento máximo vale 480Nm. é o momento de inércia calculado. Quem é ?
Cara, ele é a distância do eixo horizontal que passa pelo centroide até o ponto onde nossa tensão é calculada. A tensão vai ser máxima nas extremidades da peça mais longes desse eixo.
Sendo assim, como nossa peça é simétrica, a tensão nas extremidades vão ter valores numéricos iguais e nosso vai ser igual ao nossos raio.
Temos: