Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 150
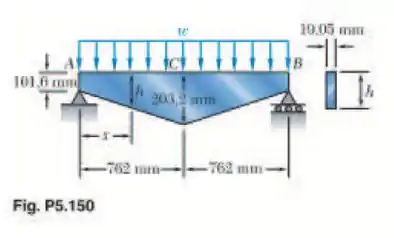
Para a viga de altura variável mostrada na figura, determine (a) a seção transversal na qual ocorre a tensão normal máxima e (b) a maior força distribuída w que pode ser aplicada, sabendo que .
Passo 1
Eaee galera, beleza? Pra resolver esse exercício, vamos primeiro determinar as reações nos apoios A e B, depois disso vamos escrever uma expressão para o momento na viga. Feito isso, o próximo passo é escrever a equação para o módulo da seção, que irá variar com x, já que a altura é variável. Depois teremos todas as informações para poder escrever a tensão normal. Com a equação da tensão, iremos deriva-la e igualar ela a zero para encontrar o ponto de tensão máxima, depois disso poderemos encontrar a maior força distribuída w que pode ser aplicada. Então vamos lá!
Passo 2
Tá legal, nesse caso, como o carregamento é simétrico, temos que as reações nos apoios A e B são iguais a metade do carregamento total, ou seja:
Agora, para encontrar a equação do momento na viga, vamos desenhar uma seção de comprimento x, onde teremos:
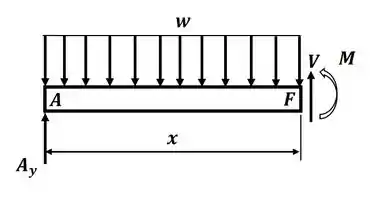
Agora, para esse DCL, vamos aplicar o somatório de momento em relação ao ponto F, para encontrar uma expressão para o momento M, então teremos:
Passo 3
Agora nós vamos escrever a expressão para a altura da seção da viga, que será dada por:
Agora, lembrando que o módulo de resistência para uma seção transversal retangular é dado por:
Substituindo a expressão que encontramos para a altura da viga, teremos:
Agora, vamos utilizar a equação 5.18 vista nessa seção para escrever o módulo de resistência da viga, que será dado por:
Então, substituindo as expressões encontradas para M e W, teremos:
Passo 4
Agora nós vamos derivar a expressão encontrada para a tensão e igualar ela a zero para encontrar o ponto de tensão máxima, então lembrando da regra do produto e da divisão para a derivada, teremos:
Agora, igualando essa expressão a zero e isolando x, teremos:
Substituindo o comprimento que é conhecido, teremos:
Belezaa! Bora pra letra (b) agora.
Passo 5
Para resolver a letra (b), vamos utilizar a equação que encontramos para a tensão em função da posição x, onde temos:
Isolando w dessa equação e substituindo os valores conhecidos, junto com a tensão admissível, teremos: