Determine o momento M que deve ser aplicado à viga de modo a criar uma tensão de compressão no ponto D, σ = 30 MPa. Além disso, trace um rascunho da distribuição de tensão que age na seção transversal e calcule a tensão máxima desenvolvida na viga.
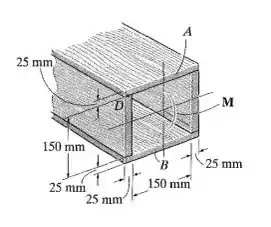
Passo 1
Gurizadaa tudo belezinha? Se liga só, o exercício pede para que possamos encontrar o momento, ele da a tensão então opaaaa!!! Vamos definir a equação:
Mas notem que temos que achar o momento , mas não temos a inércia (I) então vem comigo para encotrá-la....
A equação da inércia é definida como:
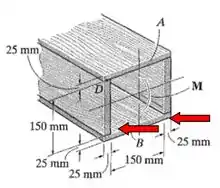
Se liga só temos a área interna e a externa, a interna notamos o comprimento de 150 mm e a externa paredes de 25 mm , então o comprimento externo: 150+25+25=200 mm
Agora temos que fazer a área externa menos a interna , vem comigo ;)
Podemos agora achar o momento M, pois temos a tensão:
Como a tensão foi dada em , podemos usar a relação:
Vamos deixar tudo em mm para conseguirmos trabalhar...
Já temos o momento, temos o momento de inércia, falta a nossa distância que vai do ponto até a linha neutra, que para o ponto vai ser:
Agora é partir pro abraço...
Passo 2
Como temos o momento, podemos calcular a tensão máxima, que será a tensão atuante na parte mais distante da linha neutra, agora a nossa distância vai ser para um ponto na extremidade...
Esboçando a distribuição de tensões na peça, temos:

Resposta
