Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 74
Determine a tensão de flexão máxima absoluta no eixo de 40 mm de diâmetro que está sujeito às forças concentradas. Os mancais de luva em A e B suportam somente forças verticais.
Passo 1
Primeiramente, para determinarmos o diagrama, precisamos das reações de apoio. Logo:
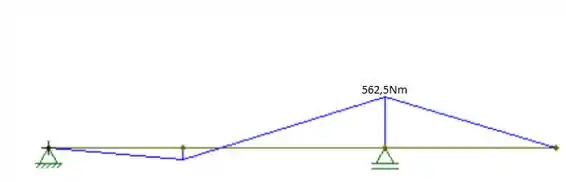
Passo 2
Logo, podemos ver que o momento máximo é 562,5Nm. Agora, podemos calcular a tensão máxima:
Resposta
Exercícios de Livros Relacionados
A viga é composta por quatro peças de madeira coladas, como mostra a figura. Se o momento fletor interno for M=120k N . m , determine a tensão de flexão máxima na viga. Trace um rascunho tridimensiona
A viga é composta por quatro peças de madeira coladas, como mostra a figura. Se o momento fletor interno for M = 120 kN.m, determine a tensão de flexão máxima na viga. Trace um rascunho tridimensional
A viga é composta por três tábuas unidas por pregos, como mostra a figura. Se o momento que age na seção transversal for M=650N . m , determine a força resultante que a tensão de flexão produz na tábu
A viga é composta por três tábuas unidas pregos, como mostra a figura. Determine as tensões de tração e compressão máximas na viga.
Sabendo-se que uma viga de seção transversal, como mostrado, é encurvada em torno de um eixo horizontal e está submetida a um momento fletor de 5,7k N ⋅ m , determinar a intensidade total da força atu