Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 12b
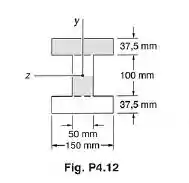
Sabendo-se que uma viga de seção transversal, como mostrado, é encurvada em torno de um eixo horizontal e está submetida a um momento fletor de , determinar a intensidade total da força atuando: (b) na porção sombreada da alma.
Passo 1
Queremos encontrar a força total sobre esse pedaço da alma. A gente pode lembrar que a força total sobre uma área pode ser escrita como:
Então, o que precisamos fazer é calcular essa integral para essa área.
Vem comigo!
Passo 2
Como nossa viga é simétrica, nosso centroide da seção fica exatamente no meio da viga, onde está a origem do nosso sistema de coordenadas na figura.
Como a largura dessa área é constante e igual a , podemos reescrever o termo:
E olhando para o eixo nossa área começa em e termina em . Aí nossa integral fica assim:
Passo 3
Precisamos achar a expressão de em função de . Podemos escrever:
Sabemos que . Precisamos achar para a seção da viga. Vamos dividir ela em 3 retângulos e calcular:
O primeiro retângulo é o que forma a base superior. Ele tem base e altura . E a gente vê que a distância do centroide desse retângulo para o centroide da seção é:
O segundo retângulo pode ser o da aba inferior. Ele vai ter as mesmas características do primeiro retângulo:
O terceiro vai ser o que forma a alma da seção. Para ela temos que:
O somatório fica:
Passo 4
Nossa expressão para fica:
E a integral fica:
Ufa! Conseguimos!