Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 82

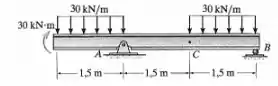
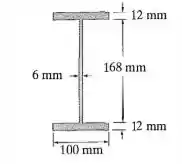
Se a viga tiver a seção transversal mostrada na figura, determine a tensão de flexão máxima

absoluta na viga.

Passo 1

Primeiramente, devemos calcular as reações de apoio. Para isso, utilizaremos as equações de equilíbrio:

∑ M a = 0 → 30 × 1,5 × 0,75 - 30 - 30 × 1,5 × 2,25 + 3 F b = 0

F b = 32,5 k N

∑ F y = 0 → F a + 32,5 - 90 = 0

F a = 57,5 k N

Montando o diagrama, temos:

Passo 2

Podemos ver que o momento máximo é igual a 30kNm. Determinando-se o momento de inércia, temos:

I = 2 0,1 × 0,012 3 12 + 0,1 × 0,012 × 0,09 2 + 0,006 × 0,168 3 12 = 2,184 × 10 - 5 m 4

A tensão máxima será:

σ m á x = 30 × 10 3 × 0,096 2,184 × 10 - 5 = 131,87 M P a

Resposta

σ m á x = 131,87 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considerando a viga do problema 76, é aplicado um momento igual ao momento plástico Mp da viga e, depois removido. Usando uma tensão de escoamento de 290 MPa, determinar a tensão residual para y1 = 25
Um momento M é aplicado à viga do problema 76, em torno do eixo z, causando zonas plásticas de 25 mm de espessura na parte superior e inferior da viga. Depois do momento ser removido determinar: (a) a
Sabendo-se que uma viga de seção transversal, como mostrado, é encurvado em torno de um eixo horizontal e está submetido a um momento fletor de 5,7k N m , determinar a intensidade total da força atuan
sabendo-se que uma viga de seção transversal mostrada é encurvada sobre um eixo horizontal, e que está submetida a um momento fletor de 4 k N m , determinar a intensidade total da força que atua na po
Resolver o P r o b4.14 , considerando que a viga é encurvada em torno de um eixo vertical por um momento de 4k N m .