Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 149
Determine a tensão de flexão máxima desenvolvida na barra se ela for submetida aos conjugados mostrados na figura. A barra tem espessura de 6 mm.
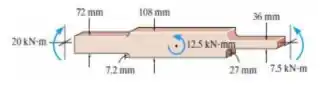
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que essa barra doidona aí tem um formato um tanto quanto diferente, já que ela se estreita de formas diferentes dos dois lados e ainda tem momentos distintos para cada um deles, e nos pede para calcular a tensão máxima. Nem parece tão difícil, é só a gente olhar para aquele ponto lá de cima e fazer. Partiu??
Passo 2
Nosso primeiro passo vai ser achar nossas relações entre a espessura () e a altura maior com a altura relativa ao ponto de momento (, que vai ser bem naquele estreitamento. Da nossa relação , teremos nosso fator de concentração de tensão (K1).
Já temos meio passo andado, ainda precisamos calcular o I1.
Agora que já achamos para o nosso lado 1, vamos achar nossas relações entre a espessura () e a altura maior com a altura relativa ao ponto de momento (, que vai ser bem naquele estreitamento. Da nossa relação , teremos nosso fator de concentração de tensão (K2).
Já temos meio passo andado, ainda precisamos calcular o I2.
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha, calcular para os dois lados e teremos o nosso momento máximo.