Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 85
Determine o momento de plastificação da seção transversal mostrada quando a viga é fletida em relação ao eixo horizontal. Admita que o material seja elastoplástico com resistência ao escoamento de
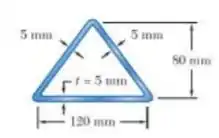
Passo 1
Fala galerinha, para resolvermos esse tipo de problema, precisamos usar um caminho diferente, no caso, queremos determinar o momento plástico, e o momento plástico para ser determinado, precisamos da LN, e o cálculo dessa LN vai ser dado da seguinte maneira:
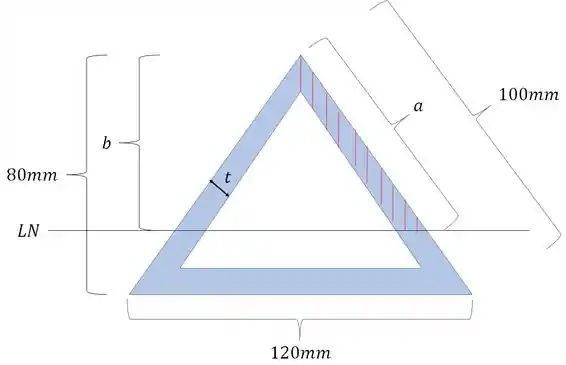
Sabemos que a área total da nossa figura é dada por:
E como nosso objetivo é determinar a nossa LN, podemos fazer a seguinte simplificação:
E para determinarmos o valor de , basta fazermos uma semelhança de triângulos.
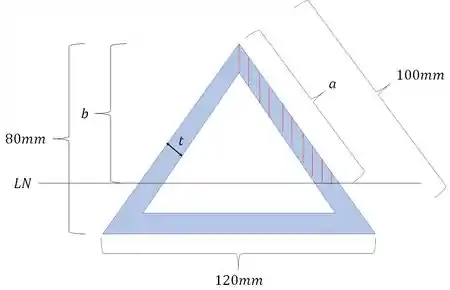
Se temos a LN, agora é só fazer o que já aprendemos para determinação do nosso momento plástico, que é definir toda a seção como sendo uma seção plastificada.
Definindo as áreas temos que:
E sabemos que a região plástica, nada mais é que a região onde a tensão de escoamento é constante, ou seja, podemos fazer o seguinte diagrama:
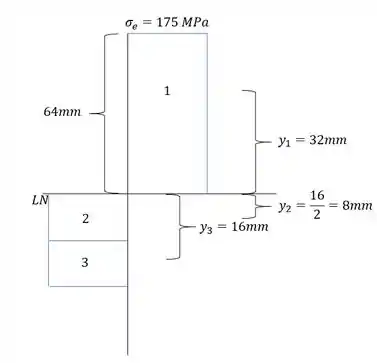
Sabemos que a força é determinada por: