Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática - 12ªEd- Ed: 14º - Capítulo 5.Problemas - Ex. 64
Determine a tração em cada cabo e as componentes da reação em D necessárias para apoiar a
carga.
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
Nesta questão vamos fazer algumas manipulações com as equações de equilíbrio. Portanto fique bem atento ao diagrama de corpo livre.
Primeiro devemos construir um diagrama de corpo livre e descobrir o valor das reações de apoio. Temos que:
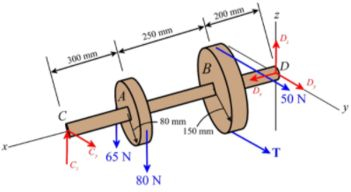
Considerando o equilíbrio de momentos em , temos que:
Resolvendo, temos que:
Para a componente em , temos que:
Resolvendo, temos que:
Para a componente em , temos que:
Passo 2
Considerando o somatório das forças em , temos que:
Para , temos que:
Sabendo que , temos que:
Para , temos que:
Como , temos que:
Resposta
Exercícios de Livros Relacionados
A estrutura de três membros é conectada em suas extremidades por meio
A estrutura de três membros é conectada em suas extremidades por meio
Uma placa circular horizontal de peso igual a 267 N é suspensa por trê
Determine as forças trativas nos cabos A B , A C e A D .
Como parte de uma verificação de seu projeto, o braço inferior de susp