Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática - 12ªEd- Ed: 14º - Capítulo 5.Problemas - Ex. 71
O membro AB é sustentado por um cabo BC e em A por um eixo retangular liso encaixado frouxamente no furo retangular da luva fixada ao membro, como na figura. Determine as componentes da reação em A e a tração no cabo necessárias para manter o membro em equilíbrio.
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
Primeiro devemos construir um diagrama de corpo livre e descobrir o valor das reações de apoio. Temos que:
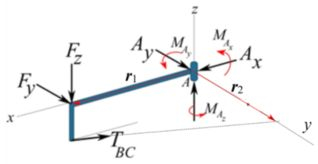
As coordenadas dos pontos , e , são:
O vetor posição é dado por:
Este vetor possui magnitude de:
Podemos então descobrir um vetor para a tensão aplicada ao longo do cabo :
Passo 2
A força que age em é dada por:
E a força que age diretamente em é dada por:
Podemos calcular o momento em :
Analisando o somatório das forças, temos que:
Logo:
Equacionando somente as componentes em , temos que:
Equacionando somente as componentes em , temos que:
Equacionando somente as componentes em , temos que:
Passo 3
Para o somatório dos momentos, temos que:
Substituindo os dados, temos que:
Resolvendo, temos que:
Rearranjando na mesma direção, temos que:
Para a componente do momento em , temos:
E: