Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 27
Determine o valor de correspondente para a posição de equilíbrio da haste do problema 10.12, quando , , e .
Passo 1
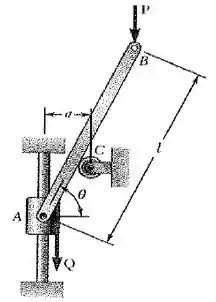
Primeiro vamos relembrar o problema 12. Onde a haste delgada AB é presa a um colar A e repousa sobre uma pequena roda em C. Desconsidere o raio da roda e o efeito do atrito.
Certo, já sabemos como é o comportamento da haste. Assim, só basta derivamos uma expressão para a magnitude da força Q necessária par manter o equilíbrio da haste. Assim, basta substituirmos os valores e teremos nossa resposta.
Passo 2
Achou um pouco complicado? Vamos destrinchar!
Observe na figura da questão que existe um triângulo , e temos o ângulo entre a hipotenusa e o cateto . Desse modo, por trigonometria, temos:
Tome:
Então:
Derivamos , teremos:
Vamos guardar essa equação por enquanto!
Passo 3
Observe agora o triângulo . Note que o ângulo entre a hipotenusa e o cateto é . Pois os triângulos e são semelhantes.
Então, podemos dizer que, olhando para o triângulo que engloba os dois:
Logo,
Do passo anterior, podemos obter:
Tome,
Então,
Derivamos essa função, obtemos:
Passo 4
Sabemos que, o trabalho virtual é 0. Ou seja,
E como,
Temos:
Logo,
Isolando, teremos:
Passo 5
Pronto! Obtemos a função, agora só substituir os valores. Sabemos que, , , e .
Portanto,