Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 4
Determine a força vertical P necessária para manter o equilíbrio da ligação no plano vertical na posição θ. Cada elo é uma barra uniforme com massa ρ por unidade de comprimento. Mostre que P é independente de θ.
Passo 1
Primeiro. vamos desenhar o diagrama de força ativa
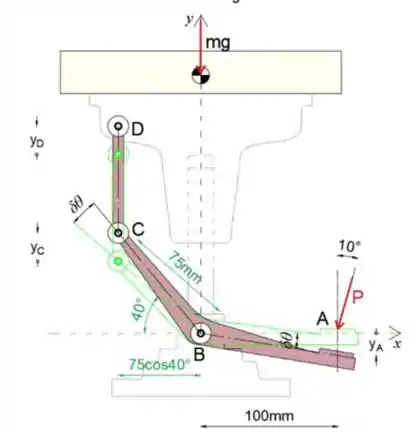
Vamos assumir que o ângulo de rotação virtual sobre o ponto B é δθ
Seguindo isso, podemos dizer que o ponto A agora se moveu verticalmente para baixo no comprimento y_A, que é igual ao produto do braço AB e o ângulo de rotação
Podemos ver no esboço que os pontos C e D, bem como parte do dispositivo conectado a D, se moverão verticalmente para cima no comprimento yC = yD, que é igual ao produto da distância horizontal entre os pontos B e C, e o ângulo de rotação
Passo 2
Sabemos que o Trabalho Virtual realizado pela força P é positivo, pois a direção da força e do deslocamento é a mesma
Substituiremos por
(1)
Enquanto o Trabalho Virtual feito por peso mg é negativo, uma vez que a direção da força e do deslocamento é oposta
Substituiremos pela expressão
(2)
Passo 3
A seguir, vamos aplicar o Princípio do Trabalho Virtual, que afirma que a soma do trabalho realizado por todas as forças ativas é igual a zero
Substituiremos e pelas expressões (1) e (2), respectivamente
Dividiremos ambos lados da equação por
A partir daqui expressaremos como
Por fim, substituiremos por and by