Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 82
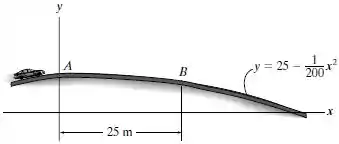
Determine a velocidade máxima que um carro de 1,5 Mg pode ter e ainda permanecer em contato com a estrada quando ele passa pelo ponro . Se o carro mantém esta velocidade, qual é a reação normal da estrada sobre ele quando ele passa pelo ponto ? Despreze a dimensão do carro.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do carro: Mg kg;
Posição do ponto : m;
Trajetória curva;
Velocidade em igual velocidade em : .
Nosso objetivo é determinar a velocidade máxima que este carro pode atingir sem que ele descole da pista no ponto . Em seguida, mantendo uma velocidade constante, esse carro passará pelo ponto , onde devemos determinar a força normal sobre ele.
Primeiramente, desenharemos o Diagrama de Corpo Livre da caixa.
Onde = força peso
= força normal resultante
= aceleração tangencial
=aceleração normal
Lembre-se que a aceleração normal deve apontar no sentido positivo do eixo normal . Como a aceleração tangencial é desconhecida, vamos supor que ela atue na direção de positiva.
Sabemos que m/s2 e que
Onde é o raio de curvatura no ponto onde o corpo está localizado.
Passo 2
Fazendo uma análise da geometria da situação, temos que
Portanto, para o ponto em m:
Para o ponto em m:
Passo 3
Em seguida, devemos encontrar o ângulo .
Olhando novamente o diagrama de corpo livre, podemos ver que
Para o ponto em m:
Para o ponto em m:
Passo 4
Agora utilizaremos a Equação do Movimento para encontrar a força em .
No ponto , queremos saber a velocidade máxima onde o carro não descola da pista. Neste caso, o valor máximo ocorrerá quando a força tender a zero, ou seja, quando o carro estiver na iminência de perder o contato com o chão. Podemos considerar então que . Logo,
Substituindo esses valores na equação de , temos
Passo 5
Agora que temos o valor de , podemos encontrar no ponto . Sabemos que
Substituindo esses valores na equação de , temos