Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 58
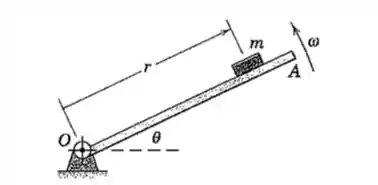
3/58) O componente giraem torno de um eixo horizontal que passa por com uma velocidade no sentido anti-horário . . Quando passa a posição , um pequeno bloco de massa é colocado sobre este a umadistância radial . Se é observado que o bloco desliza em , determine o coeficiente de atrito estático entre o bloco e o componente .
Passo 1
Bom pessoal , neste caso teremos que aplicar o princípio do somatório das forças concorrentes tanto em relaçãoas que provocam variação da velocidade angular e da velocidade tangencial . Temos que :
Da mesma forma , temos que :
Passo 2
Então galera, reparem que se dividirmos (2) por (1) , eliminamos :
Substituindo os valores que conhecemos , temos que ;
Resposta
De boa galera? Bora fazer mais exercícios então!
Exercícios de Livros Relacionados
A velocidade escalar de um satélite lançado em uma órbita circular em torno da Terra é dada pela Equação 13.25. Determine a velocidade escalar de um satélite lançado paralelo à superfície da Terra de
Um satélite de comunicações será colocado na órbita circular equatorial em torno da Terra de maneira que ele sempre permaneça diretamente sobre um ponto na superfície terrestre. Se isto exige que o pe
Um foguete está em órbita circular em torno da Terra a uma altitude de h = 4 Mm. Determine o incremento mínimo na velocidade escalar que ele deve ter a fim de escapar do campo gravitacional da Terra.
A Terra tem uma órbita com uma excentricidade e = 0,0821 em torno do Sol. Sabendo que a distância mínima da Terra ao Sol é 151,3( 10 6 ) km, determine a velocidade escalar na qual um foguete se move q
Um satélite é lançado com uma velocidade vetorial inicial v 0 = 4000k m / h paralelo à superfície da Terra. Determine a altitude necessária (ou faixa de altitudes) acima da superfície da Terra para o