Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 101

101. Um aeroplano acaba de deixar a pista com uma velocidade de decolagem v . Cada uma de suas rodas que gira livremente possui uma massa m , com um raio de giração k em relação ao seu eixo. Quando observada da frente do avião, a roda executa uma precessão na velocidade angular Ω enquanto o trem de pouso é recolhido para dentro da asa em torno da sua articulação O . Como resultado da ação giroscópica, o elemento de suporte A exerce um momento de torção M sobre B para impedir o elemento tubular de girar na luva em B . Determine M e identifique se é no sentido de M 1 ou de M 2 .

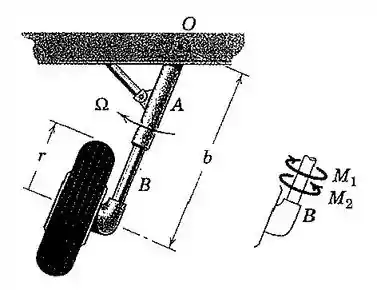
Passo 1

Primeiro, vamos montar o esquema de momentos presentes na haste da roda:

Aqui, observamos que para impedir o elemento tubular de girar em B , o momento M deve ter sentido o de M 1 .

Passo 2

Agora, vamos calcular o valor de M . Para isso, precisaremos da fórmula:

M = I Ω ⋅ p

Para começar, bora tratar de determinar o momento de inércia. Sabemos que o raio de giração k é dado pela fórmula:

k = I m

I = m k 2

E aquele nosso Ω ali, é a velocidade de precessão da roda que foi dada no enunciado.

Finalmente, para p temos que:

p = v r

M = M 1 = m k 2 Ω v r

Resposta

O sentido do momento que o suporte A exerce sobre o suporte B é o mesmo de M 1 e seu valor é de:

M 1 = m k 2 Ω v r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As abas quadradas uniformes, cada uma de massa m , são livremente articuladas em A e B à placa quadrada e o eixo associado, que giram em torno do eixo vertical z com uma velocidade angular constante ω
O disco circular fino de massa m e raio R é articulado em torno de seu eixo tangente horizontal à extremidade de um eixo, que gira em torno de seu eixo vertical com uma velocidade angular ω . Determin
O disco circular de 6 kg e o eixo associado giram a uma velocidade angular constante ω = 10000r p m . Se o centro de massa do disco está deslocado do centro em 0,05 mm, determine o módulo das forças h
A haste esbelta uniforme d comprimento l está soldada ao suporte em A na parte inferior do disco B . O disco gira em torno de um eixo vertical com uma velocidade angular constante ω que resultará em u
Se a barra semicircular do Prob. 7/81 parte do repouso sob a ação de um torque M o aplicado através do anel em torno de seu eixo de rotação z, determine o momento fletor inicial M na barra em A.