Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 105
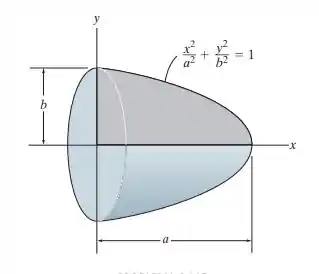
Determine o volume de um elipsoide formado girando-se a área sombreada em torno do eixo usando o segundo teorema de Pappus-Guldinus. A área e o centroide y da área sombreada devem ser obtidos primeiramente usando-se integração.
Passo 1
Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.
Este problema nos pede para determinarmos o centroide deste elipsoide. Sabemos que ele é dado por:
Primeiro, vamos determinar o volume deste elipsoide, ele é representado pelo denominador da relação que encontramos. Temos:
Onde é dado pela equação do elipsoide. Fica assim:
Substituindo:
Em seguida, vamos determinar o numerador da nossa relação:
Então, a posição do centroide vai ser dada pela razão destas integrais que calculamos, assim:
Passo 2
Em seguida, precisamos encontrar o volume pelo teorema de pappus, sabemos que ele é dado por:
Onde é o ângulo de rotação que gera o corpo, neste caso, o meio-feio. Já é área da região que vai gerar o sólido e a distância do centroide da figura até o eixo de rotação. Podemos utilizar a posição do centroide como braço de alavanca. Logo, nosso volume vai ser:
É isso, galera, Bora resolver mais questões pra ficar craque.