Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 45
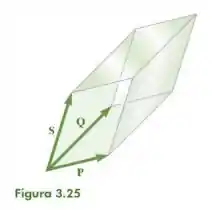
45- Determine o volume do paralelepípedo da Fig.3.25 quando e e
Passo 1
Existe um paralelepípedo cujo volume é calculado pelo produto misto de três vetores e que será dado por:
E a ordem dos termos não afeta o produto
Passo 2
Fazendo o produto vetorial da letra a temos:
Logo o produto vetorial desse vetor com será:
Onde representa unidades de volume
Passo 3
Agora para a letra b temos:
Fazendo a determinante temos:
Isso nos dá:
Agora fazendo o produto escalar com temos:
Resposta
Exercícios de Livros Relacionados
36- Desenvolva os produtos escalares B . C e B ' . C , onde B = B ' , e use os resultados obtidos para demonstrar a identidade s e nα cos β = 1 2 cos α + β + 1 2 cos α - β
38- A seção A B de uma tubulação está no plano y z e forma um ângulo de 37 com o eixo z . Os ramais C D e E F são ligados como mostrado na figura. Determine o ângulo das linhas A B e E F .
37- A seção A B de uma tubulação está no plano y z e forma um ângulo de 37 com o eixo z . Os ramais C D e E F são ligados como mostrado na figura. Determine o ângulo das linhas A B e C D .
44- O cursor P pode mover-se ao longo da barra O A . Uma corda elástica P C é ligada ao cursor e ao elemento vertical B C . Determine a distância de O até P para a qual a corda P C e a barra O A são p