Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 44
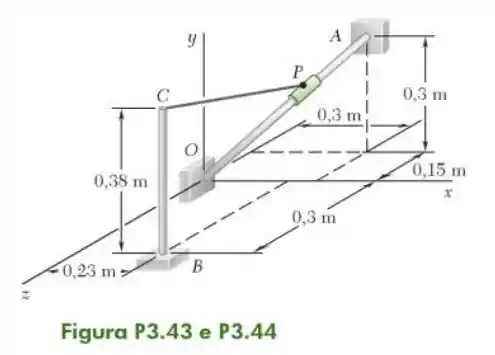
44- O cursor pode mover-se ao longo da barra . Uma corda elástica é ligada ao cursor e ao elemento vertical . Determine a distância de até para a qual a corda e a barra são perpendiculares.
Passo 1
Da questão anterior encontramos um vetor diretor igual a :
E para que haja perpendicularidade temos que ter:
Passo 2
Agora vamos supor que o ponto encontra-se no gráfico a um ponto igual a:
E pelo vetor conseguimos ver que:
O que faz então com que o vetor seja igual a:
O que é:
Passo 3
Dessa forma:
Resposta
Exercícios de Livros Relacionados
Se a intensidade da força resultante deve ser 500 N direcionada ao longo do eixo y positivo, determine a intensidade da força F e sua direção θ .
Decomponha F 2 em componentes ao longo dos eixos u e v , e determine suas intensidades.
Se θ = 60 ° e F = 450N , determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo
Decomponha F 1 em componentes ao longo dos eixos u e v , e determine suas intensidades.
Decomponha F 1 nas componentes que atuam ao longo dos eixos u e v e determine suas intensidades.