Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 38

38- A seção A B de uma tubulação está no plano y z e forma um ângulo de 37 com o eixo z . Os ramais C D e E F são ligados como mostrado na figura. Determine o ângulo das linhas A B e E F .

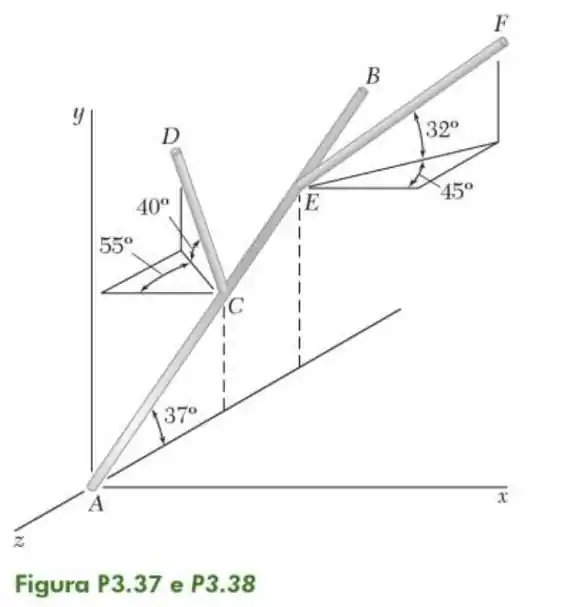
Passo 1

Agora queremos o ângulo formado entre as linhas A B e E F e para isso vamos utilizar a definição de novo.

A B → . E F → = A B . C D cos ⁡ θ

Onde os vetores A B e C D espelhados nos eixos coordenados serão iguais a:

A B → = A B 0 i + sin ⁡ 37 j + - cos ⁡ 37 k

E F → = E F cos ⁡ 32 cos ⁡ 4 5 i + sin ⁡ 32 j - cos ⁡ 32 sin ⁡ 4 5 k ]  

Passo 2

Logo se substituirmos esses resultados na nossa definição temos:

0 + A B   E F sin ⁡ 37 sin ⁡ 32 + cos ⁡ 37 cos ⁡ 32 sin ⁡ 45 = A B   E F cos ⁡ θ

cos ⁡ θ = sin ⁡ 37 sin ⁡ 32 + cos ⁡ 37 cos ⁡ 32 sin ⁡ 45

Então em graus nós iremos ter:

θ = 37.08 °

Resposta

θ = 37.08 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os cabos A B e A D ajudam a suportar o poste A C . Sabendo que a tração é 500N em A B e 160N em A D , determine graficamente a intensidade, a direção e o sentido da resultante das forças exercidas pel
A força de 1.330N deve ser decomposta em componentes ao longo das linha a - a ' e b - b ' . (a) Usando trigonometria, determine o ângulo α sabendo que o componente ao longo de a - a ' é 530N , (b) Qua
Os cabos A B e A D ajudam a suportar o poste A C . Sabendo que a tração é 500N em A B e 160N em A D , determine graficamente a intensidade, a direção e o sentido da resultante das forças exercidas pel
Um carrinho de mão que se movimenta ao longo da viga horizontal é acionado por duas forças indicadas na figura. Usando trigonometria, a intensidade, direção e sentido da força P se a força resultante
Duas são aplicadas no ponto B da viga A B . Determine graficamente a intensidade, a direção e o sentido de sua resultante usando (b) a regra do triângulo.