Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 57

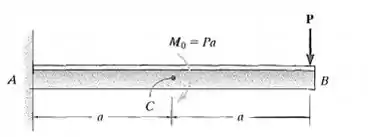
Determinea inclinação em B e a deflexão em C. EI é constante.

Passo 1

Primeiramente, vamos determinar o momento no apoio:

∑ M a = 0 → M - P a - 2 P a = 0

M = 3 P a

A equação do momento será:

M x = P x - 3 P a + P a < x - a > 0

Sabemos que:

E I d 2 v d x 2 = M x =   P x - 3 P a + P a < x - a > 0

Logo, integrando-se os 2 lados 2 vezes, temos:

E I v = P 6 x 3 - 3 P a 2 x 2 + P a 2 < x - a > 2 + C 1 x + C 2

Passo 2

As condições de contorno serão:

x = 0 → v = 0

x = 0 → d v d x = 0

Logo:

C 1 = C 2 = 0

A equação fica:

E I v = P 6 x 3 - 3 P a 2 x 2 + P a 2 < x - a > 2

Logo, a inclinação em B ( x = 2 a ) :

θ B = - 3 P a 2 E I

E a deflexão em C x = a :

∆ c = - 4 P a 3 3 E I

Resposta

θ B = - 3 P a 2 E I

∆ c = - 4 P a 3 3 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga prismática com o carregamento mostrado, determinar:A deflexão no ponto B
Para a viga com o carregamento mostrado, determinar:A deflexão no ponto E.
Para a viga com o carregamento mostrado, determinar:A declividade em B
Para a viga com o carregamento mostrado, determinar:A declividade em A;
Para a viga com o carregamento mostrado, determinar:A deflexão no ponto D.