Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 17

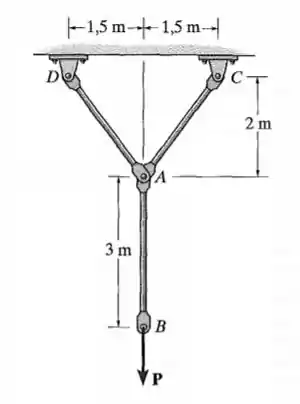
O sistema articulado é composto por três elementos de aço A - 36 conectados por pinos, cada um com área de seção transversal de 500   m m 2 . Determine o valor da força P necessária para deslocar o ponto B a uma distância de 2,5   m m para baixo.

Passo 1

Desejamos encontrar o valor da força P dada a deformação que foi descrita por B . A primeira coisa que reparamos é que as barras A C   e   A D apresentam um inclinação, então, vemos que vai ser preciso decompor essa força em duas componentes, na qual apenas a componente vertical nos interessa, dessa forma vamos ter

C = a 2 + b 2 = 1,5 2 + 2 2 = 2,5 m

Além disso o ângulo de inclinação vai ser dado por

θ = atan ⁡ a b ≈ 36,87 °

Devemos lembrar que o alongamento vai ser calculado a partir da seguinte fórmula

δ = F o r ç a   a p l i c a d a ⋅ ( c o m p r i m e n t o   e m   a n á l i s e ) M o d .   d e   e l a s t i c i d a d e ⋅ ( Á r e a   e m   a n á l i s e ) = P L E A

Passo 2

Das equações de equilíbrio tiramos que

∑ F y = 0 → F a d + F a c ⋅ s e n θ - P = 0

Da geometri do problema percebemos que F a d = F a c , dessa forma

F a d + F a c ⋅ s e n θ = P → 2 F a d = P s e n θ

Dessa forma, conseguimos calcular o alongamento das barras A B   e   A C utilizando a fórmula descrita no primeiro passo. Assim, temos

δ A - c = F a c ⋅ L a c E ⋅ A = P ⋅ L a c 2 s e n θ ⋅ E ⋅ A   e   δ b - a = P ⋅ L a b E ⋅ A

δ b = δ a + δ b - a →   δ a = δ b - P ⋅ L a b E ⋅ A

Passo 3

Dado que o ponto A se desloca devido ao alongamento, podemos estabelecer um novo ponto A ' e, então, fechamos um triângulo A A ' C e teremos

L a ' c = L a c + δ a - c

Com L A A ' = δ a   e   θ a ' = 180 ° - θ ≈ 143,13 ° , isso vai ser importante para conseguirmos encontrarmos o valor da força P porque será possível fazer através da lei dos cossenos

L a ' c 2 = δ a 2 + L a c 2 - 2 ⋅ δ a ⋅ L A c ⋅ cos ⁡ ( θ a ' )

L a c + δ a - c 2 = δ a 2 + L a c 2 - 2 ⋅ δ a ⋅ L A c ⋅ cos ⁡ ( θ a ' )

L a c + P ⋅ L a c 2 s e n θ ⋅ E ⋅ A 2 = δ a = δ b - P ⋅ L a b E ⋅ A 2 + L a c 2 - 2 ⋅ δ b - P ⋅ L a b E ⋅ A ⋅ L A C ⋅ c o s ⁡ ( θ a ' )

Resolvendo a equação para P vamos encontrar,finalmente,

P ≈ 50,47 k N

Resposta

P = 50,47   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O parafuso de aço com 10mm de diâmetro está embutido em uma luva de bronze. O diâmetro externo dessa luva é 20mm e seu diâmetro interno é 10mm . Se o parafuso for submetido a uma força de compressão P
Os cabos A B e A D de aço A- 36 tem diâmetro de 2mm , e os comprimentos dos cabos são L A C = 1,60m e L A B = L A D = 2,00m quando não carregados. Determine o diâmetro exigido para o cabo A C de modo
O elemento rígido é mantido na posição mostrada na figura por três tirantes de aço A- 36 . Cada tirante tem comprimento de 0,75m quando não alongado e área de seção transversal de 125mm 2 . Determine
O conjunto é composto por um parafuso de aço A- 36 e um tubo de latão vermelho C 83400 . Se a porca for apertada contra o tubo de modo que L = 75mm , e quando girada um pouco mais, avançar 0,02mm no p
Cada um dos três cabos de aço A- 36 tem diâmetro de 2mm e comprimentos de L A C = 1,60m e L A B = L A D = 2,00m quando não carregados. Determine a força em cada cabo depois que a massa de 150kg é susp