Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 111
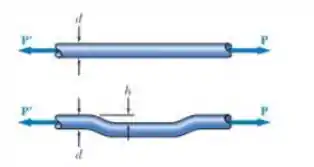
deve ser feito um desvio h em um tubo metálico de de diâmetro externo e de espessura na parede. Sabendo que a tensão máxima após criar o desvio não exceder 4 vezes a tensão no tubo quando estiver reta, determine o maior desvio a ser feito.
Passo 1
Fala galera, nosso objetivo é determinar o máximo desvio que podemos aplicar na nossa barra, e para isso, temos que o cálculo da tensão é dada por.
Para o caso da barra reta, não temos ação de momento aplicado na nossa seção, assim, podemos ignorar toda a segunda metade da nossa fórmula, assim já sabemos de cara que a tensão é dada por:
E como a base é circular, sabemos que podemos escrever a nossa equação como sendo.
Para o caso 2, o momento que a aparece é exatamente causado pelo desvio que deve ser feito, assim, temos que
A carga P que age é exatamente a carga P aplicada, assim precisamos do resto das informações da nossa barra.
Passo 2
Vamos definir o momento de inércia, a área e y, assim teremos que:
- Área da seção
- (item A)
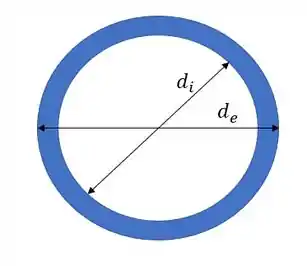
Substituondo na nossa equação temos que:
Substituindo o momento e a carga P tem-se que:
E agora vem o ponto importante, queremos que a tensão final, seja 4 vezes a tensão inicial, assim, podemos escrever que:
assim temos que:
Substituindo, temos que: