Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 110
A tábua é usada como uma trave de assoalho simplesmente apoiada. Se um momento fletor M = 1,2 kN.m for aplicado a 3º em relação ao eixo z, determine a tensão desenvolvida na tábua no canto A. Compare essa tensão com a desenvolvida pelo mesmo momento aplicado ao longo do eixo z (θ = 0º). Qual é o ângulo para o eixo neutro quando θ = 3º?
Comentário: Normalmente, as tábuas do assoalho seriam pregadas à parte superior da viga de modo que θ ~ 0º e a alta tensão devido a um mau alinhamento eventual não ocorreria.
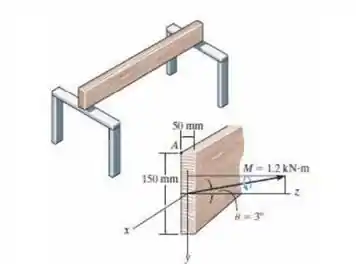
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A questão de hoje veio inspirada no halloween e já chegou tentando assustar a todo mundo. Mas, como vocês são espertos, não vão cair na pegadinha dele. Então, vamos ler com cuidado e ver o que ele pede.
Sabemos que a barra está apenas apoiada, não tendo reações de apoio nas extremidades e ele nos diz o momento fletor aplicado direto no centroide, com um ângulo de 3º em relação ao eixo Z.
Ele já nos deu o momento. Então a informação de que a barra está biapoiada desse jeito é só para gente saber que não há esforços normais.
Com esses dados, ele nos pede para calcular a tensão naquele canto superior esquerdo (mais conhecido como ponto A) e para compararmos com a tensão quando o fletor está inteiro no eixo Z.
Além de pedir também o ângulo para o eixo neutro (ou linha neutra também) quando o fletor ainda está aplicado em 3º. Parece ser muita coisa e difícil, mas vou te mostrar como é tranquilinho de fazer. Bora!
Passo 2
Nosso primeiro passo vai ser: desenhar a peça olhada de frente, ou seja, com os eixos Y e Z no plano da tela, e indicar os momentos e o ângulo α que ele pediu.
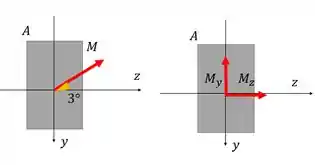
Agora que já temos nossos desenhinhos prontos, vamos decompor aquele fletor nas coordenadas Y e Z e achar o I para cada uma delas.
Passo 3
Pronto!! Temos todas as informações que precisávamos calculadas, só precisamos aplicar fórmula.
No ponto A, temos que a tensão é o somatório de todas as tensões aplicadas em cada eixo. No nosso caso, só temos as produzidas pelo fletor. Então nossa fórmulinha de tensão fica:
Nós somamos a tensão, porque ambos os momentos causam tração no ponto . Esses valores de serão a posição de em relação a cada eixo.
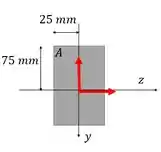
Substituindo nossos valores
Passo 4
Se o ângulo fosse igual a zero, nossa tensão seria apenas do momento sendo aplicado no eixo Z. Aí nossa fórmulinha ficaria:
Onde , já que não teríamos que decompor esse momento, porque ele já estaria no eixo z.
Passo 5
Agora, só falta calcular o ângulo com a linha neutra para o caso onde , que não é nada além de uma relação entre tangentes dada pela fórmulinha:
