Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 108
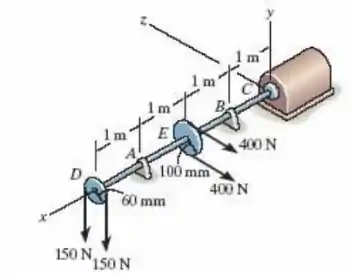
O eixo de 30 mm de diâmetro está sujeito às cargas verticais e horizontal de duas polias como mostra a figura. O eixo está apoiado em dois mancais em A e B, que não oferecem nenhuma resistência à carga axial. Além do mais, podemos considerar que o acoplamento ao motor em C não oferece nenhum apoio ao eixo. Determine a tensão de flexão máxima desenvolvida no eixo.
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? Na questão de hoje, vamos determinar tensões de flexão máxima. Mas, antes disso, vamos ver o que nosso exercício está pedindo. Ele nos conta que temos uma barra, que está apoiada nos pontos A e B, recebendo duas forças através das polias: uma horizontal e uma vertical. Como ele nos diz que o motor não oferece nenhum apoio, não temos forças naquele ponto, ele só impede que ela rotacione. Agora que já entendemos o que ele nos dá, vamos calcular a tensão de flexão máxima.
Passo 2
Então vamos lá!! Como o motor não deixa o eixo rotacionar, sabemos que o Momento em torno do ponto C é zero, assim como o somatório das forças em X e em Z. Para ficar mais fácil de sabermos para que lado cada força está atuando, vamos usar os unitários de cada eixo para representa-los, ok?? Então, teremos i para o eixo X, j para o Y e k para o Z. Pelo apoio em B, teremos duas forças de reação, uma em j e uma em k, assim como em A.
Arrumando essa bagunça, teremos:
Disso, tiramos que:
Agora que já vimos as equações do momento, vamos analisar as forças.
Na hora que solucionamos as equações, achamos:
Passo 3
Pronto!! Agora, vamos só substituir na formulinha que vimos lááááá na teoria sobre tensão de flexão e usar aqui.
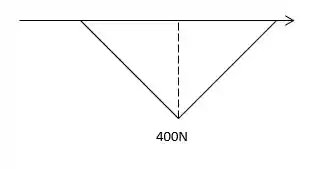
Antes, vamos montar nossos diagramas de momento, tanto para Y quanto para Z.
Momento em Y:
Momento em Z:
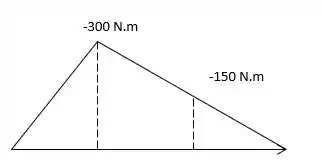
Agora que nossos diagramas estão montados, vamos pegar nossos momentos máximos em cada um deles (lembrando que, em Z, -150 é maior do que -300 – eu sei que você sabe, mas não custa relembrar) e achamos o valor máximo total.
Com o nosso M calculado, vamos jogar na nossa fórmula da tensão. Maaaas, antes disso, precisamos calcular nosso I.
Agora, finalmente, vamos achar nosso tão sonhado σ