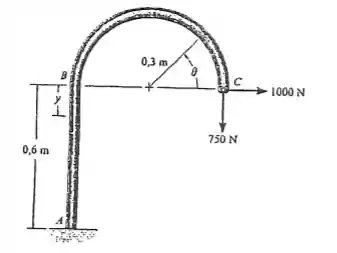
Determine a força normal, a força cortante e o momento fletor interno como uma função de 0 ° ≤ θ ≤ 180 ° e 0 ≤ y ≤ 0,6 m para o membro carregado conforme mostrado.

V = - 1000 ⋅ c o s θ + 750 sin ⁡ θ N = 1000 ⋅ s i n θ + 750 ⋅ cos ⁡ θ M = - 7 50 ⋅ 1 - c o s θ + 10 00 ⋅ sin ⁡ θ V ' = 1000 N N = - 750 N M ' = 1500 + 1000 ⋅ y

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 123

Determine a força normal, a força cortante e o momento fletor interno como uma função de e para o membro carregado conforme mostrado.

Passo 1

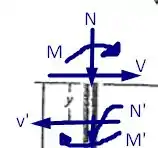
Desejamos encontrar o valor dos esforços internos como funções de . Para isso, vamos seccionar nossa figura, obtendo os seguintes diagramas de forças

Onde os ângulos destacados também valem . Além disso, podemos construir o seguinte diagrama

Passo 2

Analisando o primeiro diagrama para teremos

Quando tivermos vamos ter

Passo 3

Fazendo a mesma análise para

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a distância a entre os mancais em termos do comprimento L do eixo, de modo que o momento fletor no eixo simétrico seja zero no seu centro. A intensidade da carga distribuída no centro do eix

Determine as forças normal e cortante e o momento fletor ponto C .

Determine as forças normal e cortante e o momento fletor nos pontos A e B do elemento vertical.

Determine as forças normal e cortante e o momento fletor no ponto D da viga.

Determine a distância a entre os mancais em termos do comprimento L do eixo, de modo que o momento fletor no eixo simétrico seja zero em seu centro.