Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 119
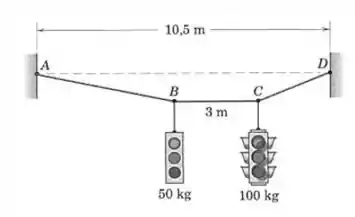
Os dois sinais de trânsito do Prob. 3/118 foram, agora, reposicionados de modo que o segmento do cabo de sustentação de tem de comprimento e está na horizontal. Especifique os comprimentos e necessários e as forças trativas em todos os três segmentos de cabo.
Passo 1
Vamos começar organizando as informações que foram dadas no enunciado, e outras que podemos deduzir pela geometria do desenho:
E essa última vem do fato de que a distância de e de até a linha pontilhada é igual.
Passo 2
Agora vamos montar algumas equações de equilíbrio para cada um dos pontos e .
Em temos o seguinte par de equações:
E para o ponto :
Passo 3
Vamos organizar isso em um sistema, lembrando que e .
E lembre: esse é um problema feito para ser resolvido no computador, do contrário é quase impossível resolver esse sistema.
Uma boa ideia é usar um programa para calcular os ângulos e numericamente:
E então você pode dividir o problema em dois. Escolhe duas das três primeiras equações para encontrar e , e três das quatro últimas equações para encontrar , e .
E para as trações:
Resposta
As forças são , , e os comprimentos são e .