Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 118
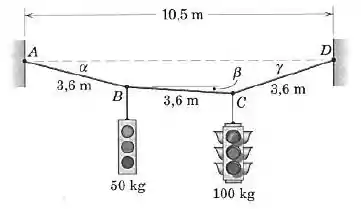
Dois sinais de trânsito estão presos, em intervalos iguais, ao cabo de sustentação de de comprimento, como mostrado. Determine os ângulos , e da configuração de equilíbrio, bem como a força trativa em cada segmento de cabo.
Passo 1
Cada um dos três pedaços do cabo terá sua própria tração, então temos , e . Além dessas três forças, temos os pesos dos dois semáforos:
O jeito mais fácil de resolver essa questão é considerar as condições de equilíbrio dos pontos e .
As forças que agem no ponto são as seguintes:
E no ponto são as seguintes:
Cada uma dessas equações vão dar origem a um sistema de duas equações!
Passo 2
Começamos com o ponto . Vamos projetar a equação nos dois eixos:
E então o sistema é o seguinte:
E agora fazemos a mesma coisa com o ponto :
E então o sistema é o seguinte:
Passo 3
Agora juntamos todas as informações:
Por enquanto temos seis variáveis e apenas quatro equações, precisamos montar mais duas. Dê uma olhada na imagem para perceber alguns detalhes geométricos:
Essa segunda equação pode ser mais dificíl de entender, mas é só notar que as “alturas” e são iguais.
Passo 4
Agora sim, temos seis variáveis e seis equações. Lembre que esse é um problema feito para ser resolvido no computador, então vamos resolver essse sistema numericamente:
Resolvendo isso em algum programa encontramos o seguinte:
E substituindo isso em três das quatro primeiras equações, encontramos:
Resposta
Os ângulos são , e . As forças são , e .