Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 156
O dispositivo "mandíbulas da vida" é usado pelos socorristas para espiar além de destroços. Uma pressão de 35 Mpa é desenvolvido atrás do pistão de raio de 50 mm. Comece determinando a força de curiosidade R, a força no elo AB, e a reação de força horizontal em C para a condição mostrada à esquerda. Então desenvolva expressões para e plotar essas quantidades como funções do ângulo da mandíbula (mostrado à direita) ao longo do intervalo. c
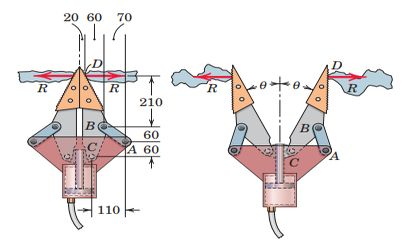
Passo 1
E ai gurizada tudo belezinha??? O exercício pede que a gente indique o valor mínimo de R e o valor para o qual este extremo ocorre.
Primeiro, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre da parte que aceita a pressão do pistão.
Precisamos calcular a força exercida no dispositivo por pressão.
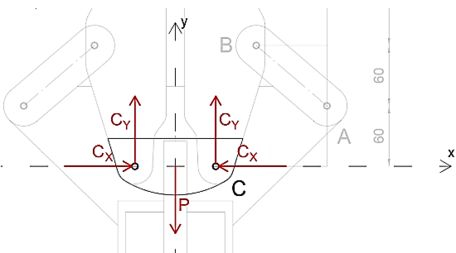
Passo 2
Usando a simetria, podemos notar que as forças de reação em ambos os pinos são iguais, portanto, podemos determinar as componentes verticais igualando a soma das forças na direção y a zero.
A seguir, desmembraremos o dispositivo e desenharemos o diagrama de corpo livre da peça BCD.
O ângulo que a força AB faz com a horizontal é
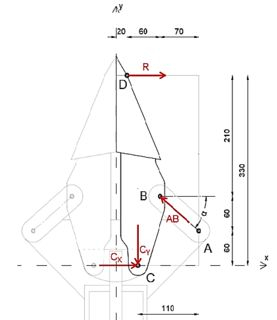
Passo 3
Equacionando a soma das forças na direção y, podemos determinar a força AB.
Equacionando a soma dos momentos sobre o ponto C a zero, eliminaremos as forças de reação em C, de modo que podemos determinar a força R.
Passo 4
Ao igualar a soma das forças na direção x, podemos determinar a força de reação
Passo 5
Começaremos por dimensionar o dispositivo e desenharemos o diagrama de corpo livre da parte BCD, já que as forças de reação continuam
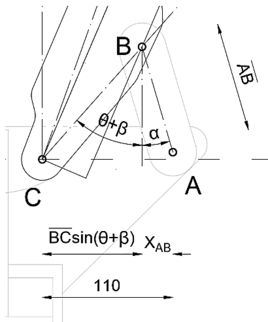
Precisamos determinar os ângulos primeiro.
Observe que a linha CE é paralela à borda da mandíbula, por isso ela faz o ângulo ... com o eixo y.
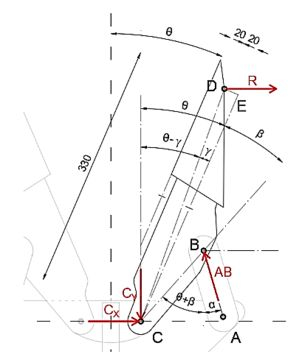
Uma vez que os pontos B e C estão na parte BCD, o ângulo é o mesmo para qualquer valor de , por isso é fácil calculá-lo
Passo 6
Também determinaremos , já que o usaremos mais tarde.
Na imagem abaixo podemos ver que o ângulo é.
Vamos agora calcular comprimentos,
Vamos substituir na expressão por seus valores.
Passo 7
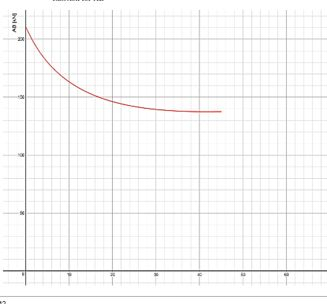
Ao igualar a soma das forças na direção y, podemos escrever a expressão para a força AB.
Usando uma calculadora gráfica como o Desmos, vamos plotar a função para AB.
Passo 8
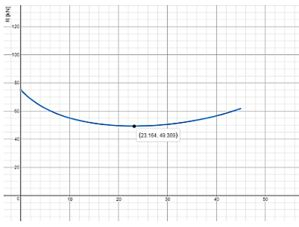
Ao igualar a soma dos momentos sobre o ponto C a zero, a única incógnita será a força R, então podemos escrevê-la como função de
Vamos colocar todos os valores conhecidos na equação.
Agora vamos substituir pela expressão anterior, respectivamente.
Passo 9
Usando uma calculadora gráfica como o Desmos, podemos que o valor mínimo para R é:
Finalmente, ao igualar a soma das forças na direção x a zero, podemos escrever a expressão para a força de reação
Uma vez que escrevemos ângulo como função de arcsin, é fácil escrever expressões para
Substituiremos AB, R e pelas expressões anteriores, respectivamente.
Passo 10
Usando uma calculadora gráfica como o Desmos, traçaremos a função para
Para
Para