Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 153

A porta de ventilação uniforme de 30 kg OAP está aberta pelo mecanismo mostrado. Trace a força necessária no cilindro DE como uma função do ângulo θ   de abertura da porta ao longo da faixa 0 ≤ θ ≤ θ m a x , onde θ m a x   é a abertura máxima. Determine o mínimo e os valores máximos desta força e os ângulos emonde esses extremos ocorrem. Observe que o cilindro não é horizontal quando θ = 0 .

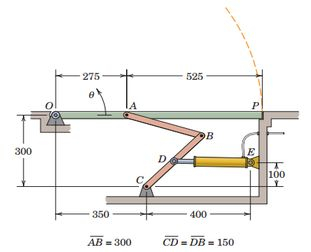
Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente determine o mínimo e os valores máximos desta força e os ângulos emonde esses extremos ocorrem. Observe que o cilindro não é horizontal quando θ = 0 .

Primeiro, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre da porta.

Observe que o peso da porta atua no ponto G.

W = m g = 30 ∙ 9.81 = 294.3   N

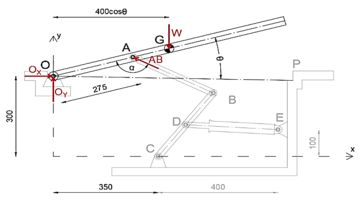
Equacionando a soma dos momentos sobre o ponto O a zero, escreveremos a expressão para AB.

∑ M o = 0

- 275   A B sin ⁡ α + 400 cos ⁡ θ ∙ W = 0

A B = 400 cos ⁡ θ ∙ W 275   sin ⁡ α

A B = 428.073 cos ⁡ θ   sin ⁡ α

Passo 2

Agora precisaremos escrever a expressão para o ângulo α .

Podemos escrevê-lo como uma soma de ângulos ε (que OA faz com AC) e φ (do triângulo isósceles ∆ C B A )

α = ε + φ

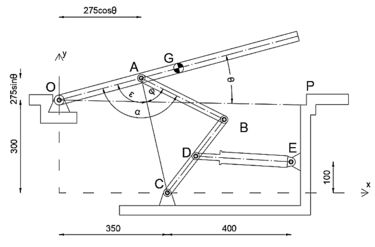
Em seguida, podemos escrever ε como a soma dos ângulos γ (que AC faz com a vertical) e 90 ° - θ (que OA faz com a vertical)

Como sabemos as coordenadas de A e C, podemos determinar γ .

γ = t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ ,   portanto, o ângulo ε é:

ε = γ + 90 ° - θ

ε = t a n - 1 350 - 275 cos ⁡ θ + 90 ° - θ 300 + 275 sin ⁡ θ

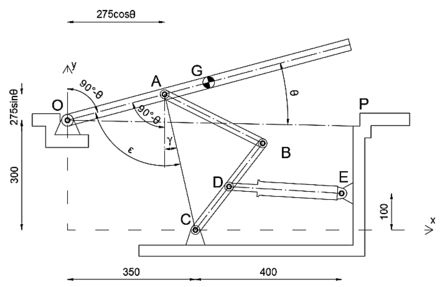
Passo 3

Olhando para a metade do triângulo ∆ C B A ( ∆ F B A ).

Podemos ver que o ângulo φ   é:

φ = arccos ⁡ A F - 300

E sabemos que AF é metade da linha AC, portanto.

A F - = 0.5   A C - = 0.5   x A C 2 + y A C 2

= 0.5   ( 350 - 275 cos ⁡ θ ) 2 + ( 300 + 275 sin ⁡ θ ) ²

= 0.5   350 2 - 192500 cos ⁡ θ + 275 2 c o s 2 θ + 275 ² s i n 2 θ ⏟ + 165000 sin ⁡ θ + 300 ² = 275 ²

= 0.25   288125 - 192500 cos ⁡ θ + 165000 sin ⁡ θ

A F - = 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ

Ângulo φ é.

φ = arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

Passo 4

Usando a regra seno, escreveremos a expressão para sin ⁡ ψ , pois ela será necessária mais tarde.

sin ⁡ ψ A C - = sin ⁡ φ 300 sin ⁡ ψ = A C - 300 sin ⁡ φ

sin ⁡ ψ = 288125 - 192500 cos ⁡ θ + 165000 sin ⁡ θ 300 sin ⁡ ( a r c c o s 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

α = ε + φ

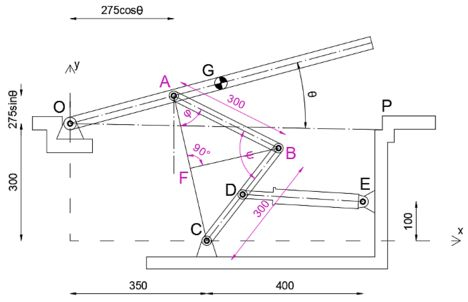
Passo 5

Vamos substituir ε por expressões anteriores, respectivamente.

α = t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + 90 ° - θ + arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

A seguir, substituiremos α pela expressão acima para obter a expressão de AB no ângulo da função θ .

A B = 428.073 cos ⁡ θ sin ⁡ α

A B = 428.073 cos ⁡ θ sin ⁡ t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + 90 ° - θ + arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

A seguir, desmembraremos o dispositivo e desenharemos o diagrama de corpo livre do membro BC.

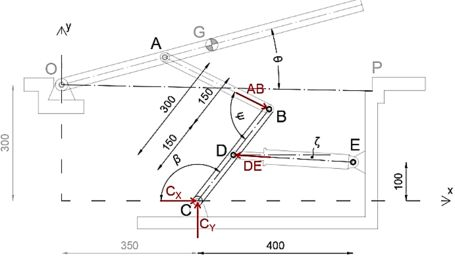
Equacionando a soma dos momentos sobre o ponto C a zero, escreveremos a expressão para DE.

∑ M c = 0

300   A B sin ⁡ ( ψ ) - 400   D E sin ⁡ ζ - 100   D E cos ⁡ ζ = 0

D E = 300   A B sin ⁡ ( ψ ) 400 sin ⁡ ζ + 100   D E cos ⁡ ζ

Agora será necessário escrever a expressão para os ângulos β .

Podemos escrever como uma soma de ângulos ε (que AC cria com o eixo x) e φ (do triângulo isósceles ∆   C B A ) .

β = δ + φ

Como sabemos as coordenadas de A e C, podemos escrever δ .

δ = t a n - 1 350 - 275 sin ⁡ θ 300 + 275 cos ⁡ θ

Também sabemos que φ é:

φ = arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

Passo 6

Portanto, a expressão para ângulo β é:

β = t a n - 1 350 - 275 sin ⁡ θ 300 + 275 cos ⁡ θ + arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

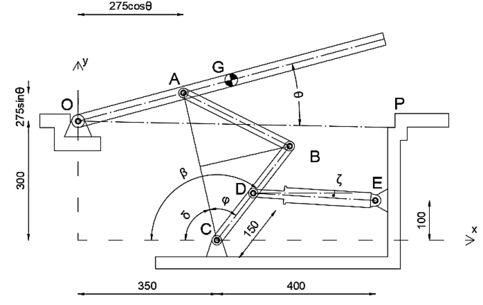
Agora substituímos AB, sin ⁡ ψ   e   ζ pelas expressões anteriores, respectivamente na equação.

D E = 300   A B   s i n   ζ   /   ( 400 sin ⁡ ζ + 100 cos ⁡ ζ )

D E = 300   ∙   428.073 cos ⁡ θ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300 sin ⁡ arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300 sin ⁡ t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + 90 ° - θ + arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300  

/ 400 sin ⁡ t a n - 1 150 sin ⁡ t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + arccos ⁡   72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300 400 + 150 cos ⁡ t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300 +

100 cos ⁡ t a n - 1 150 sin ⁡ t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + arccos ⁡   72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300 400 + 150 cos ⁡ t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

Uma vez que escrevemos a expressão para a força no cilindro DE em função do ângulo θ , tudo o que temos que fazer é determinar o domínio de nossa função, ou seja, máximo θ .

Sabemos que o ângulo será máximo quando o ponto A estiver mais alto, ou seja, quando os membros AB e CD estiverem alinhados.

Passo 7

Podemos escrever ângulo θ m a x como diferença entre ângulos 𝛇 (do triângulo ∆ O C A ) e ângulo ∠ C O P (que linha OC forma com o eixo x)

θ m a x = ζ - ∠ C O P

Usando a regra do cosseno, podemos determinar 𝛇 do triângulo ∆ O C A

O comprimento do lado OC é:

O C - = 300 2 + 350 ² = 460.98   m m

Regra de Cosene: 600 2 = 275 2 + 460.98 2 - 2.275 ∙ 460.98 cos ⁡ ζ

cos ⁡ ζ = 600 2 - 275 2 - 460.98 ² 2 ∙ 275 ∙ 460.98

ζ = arccos ⁡ 600 2 - 275 2 - 460.98 ² 2 ∙ 275 ∙ 460.98 = 106.47 °

Como sabemos as coordenadas do ponto C, é fácil determinar o ângulo ∠ C O P .

∠ C O P = t a n - 1 300 350 = 40.60 °

θ m a x = 106.47 ° - 40.60 ° = 65.87 °

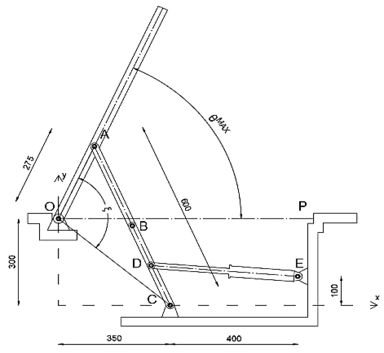
Passo 8

Usando uma calculadora gráfica, descobrimos que a força mínima DE é:

D E m i n = 0                                     N o       θ = 65.867 °

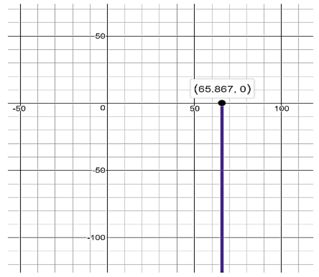
Também podemos ver que o valor máximo para DE é:

D E m a x = 3582.648   N                       N o         θ = 0 °

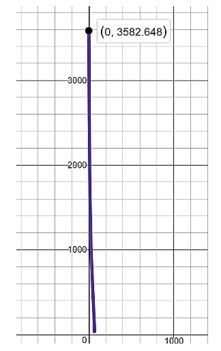
Vamos agora substituir o ângulo θ por 0° nas equações, apenas para ter certeza de que nossa solução está correta.

A B = 428.073 cos ⁡ θ sin ⁡ α

α = ε + φ

ε = t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + 90 ° - θ

ε = t a n - 1 350 - 275 cos ⁡ θ 300 + 275 sin ⁡ θ + 90 ° - 0 °

ε = 104.036 °

φ = arccos ⁡ 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

φ = arccos ⁡ 72031.25 - 48125 + 41250 ∙ 0 300 = 58.98 °

α = 104.036 ° + 58.98 ° = 163.016 °

A B = 428.073 sin ⁡ 163.016 = 1465.48   N

D E = 300   A B sin ⁡ ( ψ ) 400 sin ⁡ ζ + 100   D E cos ⁡ ζ

β = δ + φ

δ = t a n - 1 350 + 275 sin ⁡ θ 300 - 275 cos ⁡ θ

δ = t a n - 1 300 350 - 275 = 75.96 °

β = 75.96 ° + 58.98 ° = 134.94 °

ζ = t a n - 1 150 sin ⁡ β - 100 400 + 150 cos ⁡ 134.94 °

ζ = t a n - 1 150 sin ⁡ 134.94 ° - 100 400 + 150 cos ⁡ 134.94 ° = 1.20 °

sin ⁡ ψ = 288125 - 192500 cos ⁡ θ + 165000 sin ⁡ θ 300 sin ⁡ ( a r c c o s 72031.25 - 48125 cos ⁡ θ + 41250 sin ⁡ θ 300

sin ⁡ ψ = 288125 - 192500 300 sin ⁡ ( a r c c o s 72031.25 - 48125 300 = 0.8833

D E = 300 ∙ 1465.48 ∙ 0.8833 400 sin ⁡ 1.20 ° + 100 cos ⁡ 1.20 °

D E m a x = 3584   N   ≈ 3582.648   N

Resposta

D E m i n = 0                                                                 N o   θ = 65.867 °

D E m a x = 3584.648   N                       N o   θ = 0 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dobrador de barra para formar aço de reforço consiste na alavanca OAB articulada em O à placa de base fixa. Os rolos formadores em A, O e C são todos livres para girar. Para a posição 60 ° mostrada,
Cada um dos suportes de pouso de uma espaçonave de exploração de planetas é projetado como uma treliça espacial simétrica em relação ao plano x-z vertical, conforme mostrado. Para uma força de aterris
Para uma dada força P no manípulo do grampo articulado, a força de aperto C aumenta para valores muito grandes à medida que o ângulo θ diminui. Para P = 30 lb, determine a relação entre C e θ e plote-
O dobrador de barra para formar aço de reforço consiste na alavanca OAB articulada em O à placa de base fixa. Os rolos formadores em A, O e C são todos livres para girar. Para a posição 60 ° mostrada,
Determine e plote as forças nos três membros da treliça simples para valores de θ no intervalo 0≤ θ 120 ° . O que acontece se for superior a 120 ° ? Para fins de plotagem, considere as forças de traçã