Na posição especial mostrada para o guincho, as barras AF e EG estão em ângulos retos entre si e AF é perpendicular a AB. Se a talha estiver manuseando uma tora pesando 4800 lb, calcule as forças suportadas pelos pinos em A e D nesta posição devido ao peso da tora.
Passo 1
Primeiro, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre da peça EG
Força ED faz o ângulo α com a linha EG
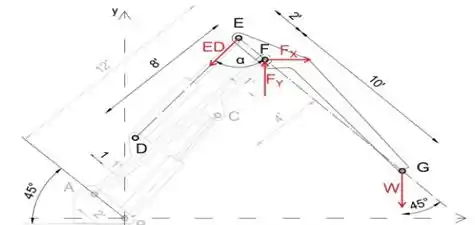
Passo 2
Ao igualar a soma dos momentos sobre o ponto F a zero, eliminaremos as forças de reação em F, para que possamos determinar a força ED
Observe que a reação em D é igual à força no cilindro ED, o que pode ser facilmente mostrado analisando a junta D
Equacionando a soma das forças na direção x - e y - a zero, determinaremos as forças de reação em F
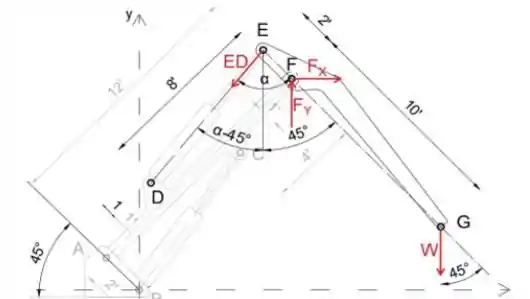
Passo 3
Próximo. vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre da parte ADCF
Observe que as linhas DE e BC são paralelas, bem como as linhas EG e AB, portanto, a força BC faz o ângulo α com a linha AB
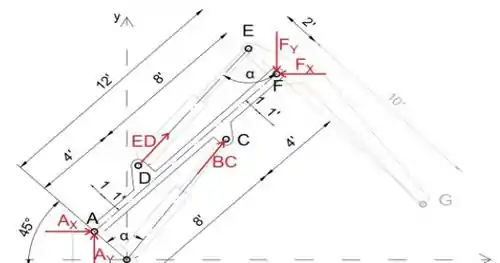
Passo 4
Equacionando a soma dos momentos sobre o ponto A a zero, eliminamos as forças de reação em A, para que possamos determinar a força de reação BC
Equacionando a soma das forças na direção x e y a zero, determinaremos as forças de reação em A
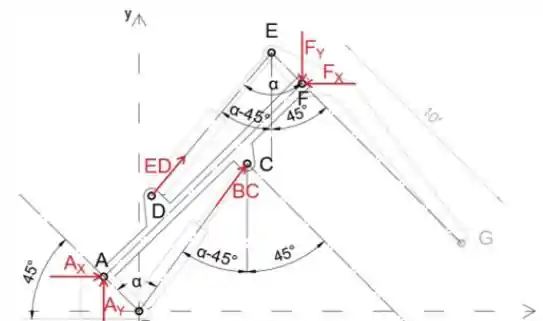
Use o teorema de Pitágoras para determinar a magnitude da força A