Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 60
Se , determine o menor coeficiente de atrito estático entre os colares e e a barra necessário para que o sistema permaneça em equilibrio, independente do peso do cilindro . As ligações e possuem peso desprezível e estão conectados em por um pino.
Passo 1
O problema pede que descubra o menor coeficiente de atrito estático entre e para que o sistema fique em equilibrio.
Bom galera, a a gente percebe que a figura do problema é simétrica, então a gente pode analisar só um lado separado, vamos fazer o diagrama de corpo livre do lado .
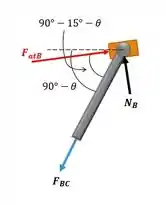
A força de atrito estático em é:
Passo 2
Agora, se a gente prestar atenção tá perpendicular á então eles não atuam na direção um do outro.
Então a força que equilibra é a componente em de , bem assim:
Passo 3
Beleza, agora na direção do atrito, as forças que se equilibram são a de atrito em com a componente de em :
E a gente consegue calcular as duas forças com o que a gente já encontrou, bem assim:
A gente pode eliminar que tá multiplicando os dois lados, fica assim: