Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 129

Determine os componentes da reação em A para o quadro de espaço carregado mostrado. Cada conexão pode ser tratada como uma junta esférica.

Passo 1

Primeiro, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre do membro BE

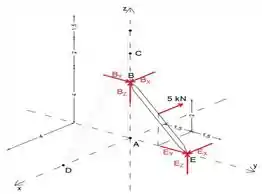
Equacionando a soma dos momentos sobre o eixo z a zero, determinaremos a força de reação EX

∑   M Z = 0 1.5 ⋅ 5 - 3 E X = 0 E X = 7.5 3 E X = 2.5 k N

Ao igualar a soma das forças na direção x a zero, calcularemos a força de reação BX

∑ F X = 0

B X + E X - 5 = 0 B X = 5 - E X B X = 5 - 2.5 B X = 2.5 k N

Ao igualar a soma das forças na direção z a zero, escreveremos a força de reação EZ como função de BZ

∑ F Z = 0

B Z + E Z = 0 E Z = - B Z                                                     ( 1 )

Ao igualar a soma dos momentos sobre o eixo x a zero, escreveremos a conexão entre as forças de reação EZ e BY

∑   M X = 0 3 E Z - 4 B Y = 0 E Z = 4 3 B Y

Podemos substituir EZ pela expressão (1)

- B Z = 4 3 B Y B Z = - 4 3 B Y                                               ( 2 )

Passo 2

A seguir, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre do membro ABC

Observe que o membro CD com o eixo y faz o ângulo de

α = t a n - 1 ⁡ 4 6 = 33.69 ∘

Equacionando a soma dos momentos sobre o eixo x a zero, determinaremos a força de reação BY

∑ M X = 0

6 ⋅ 7.5 - 4 B Y = 0 B Y = 6 ⋅ 7.5 4 B Y = 11.25 k N

Colocando o valor de CY na expressão (2), podemos calcular a força de reação CZ

B Z = - 4 3 B Y                                                               ( 2 ) B Z = - 4 3 ⋅ 11.25 B Z = - 15 k N

Equacionando a soma dos momentos sobre o eixo y a zero, calcularemos a força no membro CD

∑ M Y = 0

- 6 C D s i n ⁡ 33.69 ∘ - 4 B X = 0 C D = 4 B X 6 s i n ⁡ 33.69 ∘ C D = 4 ⋅ 2.5 6 s i n ⁡ 33.69 ∘ C D = - 3.00 k N

Passo 3

Finalmente, ao igualar a soma das forças na direção x, y e z a zero, determinaremos as forças de reação no ponto A

∑ F X = 0

A X - C D s i n ⁡ 33.69 ∘ - B X = 0 A X = C D s i n ⁡ 33.69 ∘ + B X A X = - 3.00 s i n ⁡ 33.69 ∘ + 2.50

A X = 0.83 k N

∑ F Y = 0

A Y - B Y + 6 = 0 A Y = B Y - 6 A Y = 11.25 - 6

A Y = 5.25 k N

∑ F Y = 0

A Z + C D c o s ⁡ 33.69 ∘ - B Z = 0 A Z = B Z - C D c o s ⁡ 33.69 ∘ A Z = - 15 - ( - 3.00 ) c o s ⁡ 33.69 ∘

A Z = - 12.50 k N

Resposta

A X = 0.83 k N A Y = 5.25 k N A Z = - 12.50 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dispositivo “mandíbulas da vida” de Prob. 4/88 é redesenhado aqui com suas mandíbulas abertas. A pressão atrás do pistão P de área de 20 in² é mantida em 500 l b / i n . 2 Calcule e plote a força R
Determine e plote as forças em todos os membros da treliça simples carregada como funções do ângulo ao longo do intervalo 0≤ α≤ 90 ° . Indique os valores mínimos para as forças nas barras AC e CD e os
O caminhão mostrado é usado para entregar alimentos para aeronaves. A unidade elevada pesa 2.000 libras com centro de gravidade em G. Determine a força necessária no cilindro hidráulico AB.
Calcule os componentes x e y de todas as forças que atuam em cada membro do quadro carregado.
O ângulo da superfície de suporte em C pode variar de 0 (vertical) a 90∘ (horizontal). (a) Trace a força no membro BC como uma função de θ neste intervalo. Observe quaisquer condições incomuns.(b) Par