Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 128
O projeto de um mecanismo de içamento para o caminhão basculante é mostrado na visão ampliada. Determine a compressão P no cilindro hidráulico BE e a magnitude da força suportada pelo pino em A para a posição particular mostrada, onde BA é perpendicular a OAE e o elo DC é perpendicular a AC. O despejo e sua carga juntos pesam 20.000 lb com centro de gravidade em G. Todas as dimensões para a geometria indicada são fornecidas na figura.
Passo 1
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da força de despejo no membro CD e as forças de reação em O agindo nele.
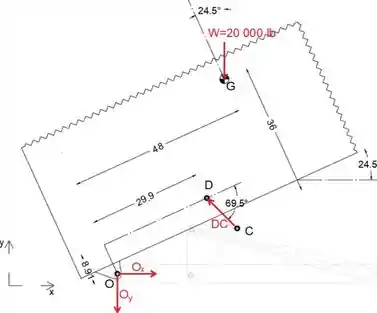
Equacionando a soma dos momentos sobre o ponto O a zero, podemos determinar a força DC
Daqui podemos expressar a força DC como
Passo 2
Primeiro, vamos isolar e desenhar o diagrama de corpo livre do triângulo ABC
Observe que BE faz com o ângulo horizontal de:
Uma vez que a distância entre pontos A e C é
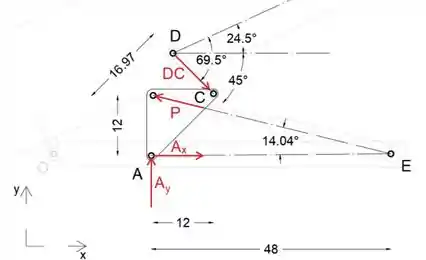
Equacionando a soma dos momentos sobre o ponto A a zero, podemos determinar a força P
A partir daqui, podemos expressar P como:
Substitua DC por seu valor
Passo 3
Ao igualar a soma das forças na direção x – e y - a zero, podemos determinar as forças de reação em A
Substitua P e DC por seus valores
Substitua P e DC por seus valores
Finalmente, usando o teorema de Pitágoras, podemos calcular a magnitude da força atuando no pino A