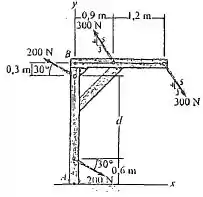
90. Dois binários agem sobre a estrutura. Se , determine o momento de binário resultante. Calcule o resultado decompondo cada força em componentes e e

(a)encontrando o momento de cada binário (Equação 4.13)

Vamos começar calculando o momento binário do par de forças Precisamos da sua forma vetorial, e assim, das suas componentes em e .

Para decompor em , vamos usar o triângulo retângulo dado em sua orientação. Como o lado que vale é paralelo ao eixo , para achar a componente da força nesse eixo, multiplicamos o módulo da força por , assim:

Ela fica negativa, porque estamos olhando para a força de que está mais a direita. Ela está apontando para o sentido negativo de .

Já a sua coordenada em fica

Isso porque o lado do triangulo é paralelo ao eixo e essa componente aponta para o sentido positivo do eixo.

Nosso vetor fica:

O vetor entre essas forças pode ser achado da seguinte maneira: nós achamos a distância entre as linhas de ação das nossas forças. Pela figura, essa distância vale . Aí a gente coloca a componente que representa o eixo paralelo a essa distância.

Como nossa distância entre a linha de ação das forças está paralelo a , usamos o vetor unitário . Aí nosso vetor fica:

Só podemos fazer isso porque escolhemos a força mais a esquerda.

E o momento binário é:

Agora vamos calcular o momento em relação ao par de . Vamos achar o vetor da força que está mais acima. As componentes dela são:

A componente é negativa porque a força aponta para o sentido negativo de .

O vetor da força é

E o vetor vai ser achado usando o mesmo bizu do passo anterior. A distância entre a linha de ação das forças é . Já que essa distância é paralela a , nosso vetor fica

Só podemos fazer isso porque escolhemos a força mais acima.

Assim, o momento desse par é

Vamos calcular o momento binário resultante:

Calculando:

Assim