Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 65
Uma chave de roda é usada para apertar um parafuso de cabeça quadrada. Se forças de forem aplicadas à chave, como mostrado, determine o módulo das forças iguais exercidas nos quatro pontos de contato na cabeça de do parafuso, de modo que seu efeito externo sobre o parafuso seja equivalente ao das duas forças de . Considere que as forças são perpendiculares aos lados planos da cabeça do parafuso.
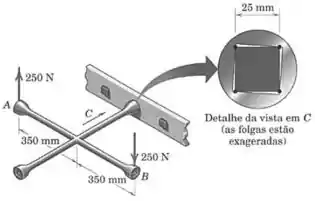
Passo 1
Vamos começar calculando o momento gerado pelas forças aplicadas à chave de roda. Como essas duas forças tem mesmo módulo e direção, mas sentidos opostos, elas formam um binário:
E agora queremos saber qual deve ser o módulo de quatro forças exercidas sobre as bordas do parafuso para que o momento gerado seja o mesmo.
Passo 2
Já que a ideia é gerar uma rotação no sentido horário (para quem olha de frente para a cabeça do parafuso), as forças tem que ser aplicadas nas seguintes direções:
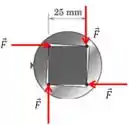
Perceba que o que temos aí na verdade são dois binários, pois podemos formar dois pares de forças com mesmo módulo e direção, mas sentidos opostos. Então o momento gerado por essas forças é o seguinte:
E agora só precisamos igualar isso ao momento gerado pela chave de roda:
Resposta
As forças devem ter módulo de .