Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 67
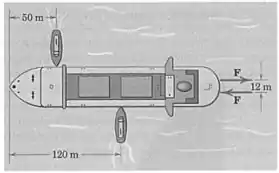
Cada hélice de um navio de duas hélices desenvolve um empuxo de na velocidade máxima. Ao manobrar o navio, uma hélice está girando a toda velocidade para frente e a outra a toda velocidade no sentido reverso. Que empuxo cada rebocador deve exercer no navio para contrabalançar o efeito das hélices?
Passo 1
O par de forças separadas por uma distância de formam um binário:
Se os rebocadores vão contrabalançar o efeito das hélices, eles precisam gerar um binário de mesmo módulo, no sentido contrário.
Passo 2
Olhando para a figura podemos ver que a distância entre as linhas de ação da força de cada rebocador é:
E então, para que haja equilíbrio:
Resposta
O empuxo de cada rebocador deve ser .
Exercícios de Livros Relacionados
Um avião comercial com quatro turbinas a jato, cada uma produzindo um empuxo à frente de 90k N , estpa em um vôo de cruzeiro, estacionário, quando o motor número 3 falha repentinamente. Determine e lo
Na posição em equilíbrio mostrada, a resultante das três forças atuando na haste dobrada passa pelo mancal O . Determine a força vertical P → . O resultado depende de θ ?
A polia e a correia em V presa a ela estão girando no sentido anti-horário e estão submetidas à carga de 1600N , devida aos dentes da engrenagem, e aos esforços trativos de 800N e 450N na correia em V
Para essa viga, as especificações de projeto para o encaixe em A dependem do módulo e da posição das cargas aplicadas. Represente a resultante das três forças e do momento por uma única força R → em A
Duas polias estão submetidas às forças trativas das correias, como mostrado. Se a resultante R → dessas forças passa pelo centro O , determine T → , o módulo de R → e o ângulo anti-horário θ que R → f