Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 60
O sistema força-binário indicado está aplicado a um pequeno eixo localizado no centro da placa. Substitua esse sistema por uma única força e especifique a coordenada do ponto sobre o eixo através do qual passa a linha de ação dessa força resultante.
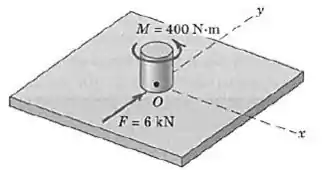
Passo 1
Na situação inicial, o momento da força em relação a é nulo, já que a linha de ação da força passa pelo ponto .
Então o único momento com que temos que nos preocupar, é o . E a única força resultante, é a de na direção de .
Isso já responde a primeira parte da pergunta, a nossa força resultante tem que ser:
Não se esqueça de que a expressão de um vetor não muda quando o transaladamos, por isso é normal que seja idêntico a , afinal nós só estamos mudando o ponto sobre o qual é aplicado.
Passo 2
Beleza, agora nós temos que garantir que essa força produza o momento de . Podemos ajustar isso escolhendo a posição certa em que será aplicada.
Onde é a distância entre o ponto de aplicação de (sobre o eixo ) e o ponto :
Pronto! Se aplicarmos nessa posição o efeito final vai ser o mesmo que tínhamos no caso ilustrado na figura.
Resposta
A força deve ser e a linha de ação da força deve cruzar o eixo em .