Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 20

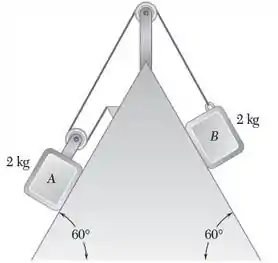
Dois blocos idênticos são liberados em repouso. Desprezando a massa das roldanas e sabendo que os coeficientes de atrito estático e cinético são μ s = 0,30 e μ k = 0,20 , determine (a) a velocidade do bloco B depois deste ter movimentado 2 m, (b) a tração no cabo.

Passo 1

Fala aê!! Tudo beleza? Neste problema devemos encontrar a velocidade do bloco B depois deste ter movimentado 2 m (item a) e a tração exercida no cabo (item b).

Antes de resolvermos os itens a e b, devemos checar se os blocos se movem.

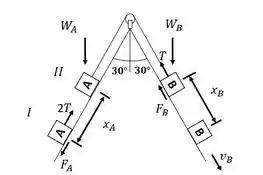
Bloco B:

↗ ∑ F = N B - m B g s e n 30 ° = 0

N B = g

↖ ∑ F = T - m B g c o s 30 ° + F B f = 0

F B f = μ s N B = 0,3 g

T = 2 g ⋅ 3 2 - 0,3 g

T = ( 3 - 0,3 ) g →   Situação I

Bloco A:

↖ ∑ F = N A - m B g s e n 30 ° = 0

N A = 2 g 1 2 = g

↗ ∑ F = 2 T - m A g c o s 30 ° + F A f = 0

F A f = 2 T - 2 g ⋅ 3 2 →   Situação I I

Substituindo T de I em I I

F A f = 2 3 - 0,3 g - 2 g ⋅ 3 2 = 1,132 g

Requisito para o equilíbrio:

F A f = 1,132 g

O atrito máximo em A é:

A = μ s N A = 0,3 g

Como 0,3 g < 1,132 g , o bloco se move. Agora estamos prontos para responder os itens a e b.

Passo 2

(a)

F B f = μ k N B = 0,20 g

F A f = μ k N A = 0,20 g

T 2 = 1 2 m A v A 2 + 1 2 m B v B 2 = 1 2 2 v B 2 4 + v B 2

T 2 = 5 4 v B 2

OBS: x A = 1 e x B = 2

U 1 → 2 = - m A g c o s 30 ° x A + m B g c o s 30 ° x B - F A f x A - F B f x B

U 1 → 2 = - 2 3 2 1 + 2 3 2 2 - 0,2 f 1 - 0,2 f 2 [ 9,81 ]

U 1 → 2 = 1,732 - 0,6 9,81 = 11,105   J

T 1 + U 1 → 2 = T 2

0 + 11,105 = 1,25 v B 2

v B = 2,98   m / s

Passo 3

(b) T 2 = 1 2 m B v B 2 = 1 2 2 2,98 2

T 2 = 8,88   J

N B = m B g s e n 30 ° = 9   N

U 1 → 2 = m B g c o s 30 ° x B - ( T ) ( 2 ) - F B f x B

U 1 → 2 = 2 ( 9,81 ) 3 2 2 - 2 T - ( 0,2 ) ( 9 ) ( 2 )

U 1 → 2 = 2 3 g - 2 T - 0,4 g

T 1 + U 1 → 2 = T 2

0 + 2 3 g - 2 T - 0,6 g = 8,88

2 T = 2 3 - 0,4 g - 8,88 = 21,179

T = 10,59   N

Resposta

(a) 2,98   m / s

(b)   10,59   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco de 375 N (massa =37,5 kg) é solto do repouso 1,5 m acima da placa. Determine a compressão de cada mola quando o bloco instantaneamente chega ao repouso após bater na placa. Despreze a massa da
Resolva o problema 14.18 utilizando a equação de conservação da energia
Cada uma das duas tiras de elástico do estilingue tem um comprimento não deformado de 200mm. Se elas são puxadas para trás para a posição mostrada e soltas do repouso, determine a altura máxima que o
Resolva o problema 14.7 utilizando a equação de conservação de energia
O bloco A tem massa de 0,75 kg e desliza na ranhura horizontal lisa. Se o bloco é recuado para s=0,45 m e solto do repouso, determine sua velocidade no instante s=0. Cada uma das duas molas tem uma ri