Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 58
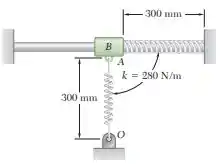
Um colar de 5 kg pode deslizar sem atrito ao longo da haste horizontal e está em equilíbrio em quando ele é puxado 125 mm para a direita e liberado. O comprimento indeformado de cada mola é 300 mm e a constante de cada mola é . Determine (a) a máxima velocidade do colar, (b) a máxima aceleração do colar.
Passo 1
Vamos lá! Vamos começar resolvendo a letra a), em que precisamos determinar a máxima velocidade do colar. Para isto, iremos utilizar o princípio de conservação de energia, que nos diz que:
De início sabemos que o bloco partirá do repouso. Portanto, .
Como queremos que a velocidade seja máxima, será necessário que a energia potencial, a qual tem apenas componente elástica nesta questão (não há variação de altura), seja mínima no ponto 2.
De fato, o ideal é que ela fosse nula. E, no caso desta questão, isto é possível quando o colar passa pelo ponto . Portanto, temos que . Agora, nos resta calcularmos o potencial inicial
Passo 2
Para calcularmos a energia potencial elástica inicial, precisamos calcular a deformação inicial de cada mola. A partir da geometria do problema, temos:
Portanto, a energia potencial inicial será:
Para finalizarmos a letra a), vamos determinar a velocidade máxima. Utilizando a conservação de energia, temos:
Passo 3
Agora temos que resolver a letra b). Aqui, precisamos determinar a aceleração máxima do colar, a qual ocorrerá quando a força submetida seja máxima.
No caso da questão, a força é máxima quando a deformação é máxima. Desta forma, temos que analisar as forças na direção horizontal (direção de movimentação) a partir do ponto inicial, quando a deformação é máxima.
Para nos auxiliar, vejamos o diagrama de corpo livre do problema:
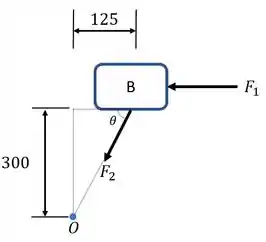
Sendo a força associada a mola horizontal, que deforma e associado a outra mola que deforma . Portanto, as forças são:
Portanto, a aceleração máxima na direção horizontal será:
E assim finalizamos a questão.