Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas de Revisão - Ex. 128

O pino B de 4 oz desliza ao longo da fenda no braço giratório OC e ao longo da fenda DE de raio b = 20 in que foi aberta em um plano horizontal fixo. Desprezando o atrito e considerando θ = 15   r a d / s   θ ¨ = 250   r a d / s para a posição θ = 20 ° , determine para esta posição (a) os componentes radial e transversal da força resultante exercida sobre o pino B, (b) as forças P e Q exercidas sobre o pino B respectivamente pelo braço OC e pela parede da fenda DE.

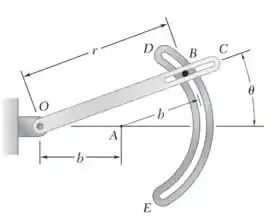
O pino B de 110 g desliza ao longo da fenda no braço giratório OC e ao longo da fenda DE de raio b 500 mm que foi aberta em um plano horizontal fixo. Desprezando o atrito e considerando 15 rad /s e 250 rad /s² para a posição 20°, determine para esta posição (a) os componentes radial e transversal da força resultante exercida sobre o pino B, (b) as forças P e Q exercidas sobre o pino B respectivamente pelo braço OC e pela parede da fenda DE.

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine os componentes radial e transversal da força resultante exercida sobre o pino B, (b) as forças P e Q exercidas sobre o pino B respectivamente pelo braço OC e pela parede da fenda DE. Então vem comigo :D

Cinematica.

Do desenho do sistema, nós temos

r = 2 b c o s θ

Então

r = - ( 2 b s e n θ ) θ ˙

e

r ¨ = - 2 b ( θ ¨ s e n θ + θ ˙ 2 c o s θ )

Agora

a r = r ¨ - r θ ˙ ² = - 2 b ( θ ¨ s e n θ + θ ˙ 2 c o s θ ) - ( 2 b c o s θ ) θ ˙ 2

= - 2 b ( θ ¨ s e n θ + 2 θ ˙ 2 c o s θ )

= - 2 500 12 [ ( 250   r a d / s ² ) s e n 20 ° + 2 ( 15   r a d / s ) ² c o s 20 ° ] = 1694.56   m / s ²

e

a θ = r θ ¨ + 2 r ˙ θ ˙ = ( 2 b c o s θ ) θ ¨ + 2 ( - 2 b θ ˙ s e n θ ) θ ˙ = 2 b ( θ ¨ c o s θ - 2 θ ² ˙ s e n θ )

= - 2 500 12 [ ( 250   r a d / s ² ) c o s 20 ° - 2 ( 15   r a d / s ) ² s e n 20 ° ] = 270.05   m / s ²

Passo 2

Cinética.

(a)Nós temos

F r = m a r = 1 4 10   m / s ² × ( - 1 694.56 / s ² ) = - 13.1565   N

ou

F r = - 13.16   N

e

F θ = m a θ = 1 4 10 f t / s ² × ( 270.05 m / s ² ) = 2.0967   N

Ou

F θ = 2.10   N

Passo 3

(b)

+   Σ F r :   - F r =   - Q c o s 20 °

ou

Q = 1 c o s 20 ° ( 13.1565   ) = 14.0009  

ou

+   Σ F θ :   - F θ =   P - Q s e n 20 °

P = 2.0967 + 14.0009 s e n 20 ° l b = 6.89  

Resposta

a :   F r = - 13.16   N

a :   F θ = 2.10   N

b : P = 6.89   l b   ∢   70 °

b : Q = 14.00   ∢   40 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco B de 12 lb repousa, tal como mostra a figura, sobre a superfície superior de uma cunha A de 30 lb. Desprezando o atrito, determine, imediatamente depois que o sistema é solto a partir do repo
A pista de montanha-russa mostrada na figura está contida em um plano vertical. A parte da pista entre A e B é reta e horizontal, enquanto as partes à esquerda de A e à direita de B têm raios de curva
Mostre que o raio r da órbita da Lua pode ser determinado pelo raio R da Terra, a aceleração da gravidade g na superfície da Terra e o tempo necessário para lua completar um volta em torno da Terra. C
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se move sob a ação da força central F dirigida para fora do centro de força O. Sabendo que a part
O disco A gira em um plano horizontal em torno de um eixo vertical a uma taxa constanteθ = 12 r a d / s . O cursor B tem uma massa de 230 g e se movimenta em uma fenda sem atrito aberta no disco. O cu