Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 14

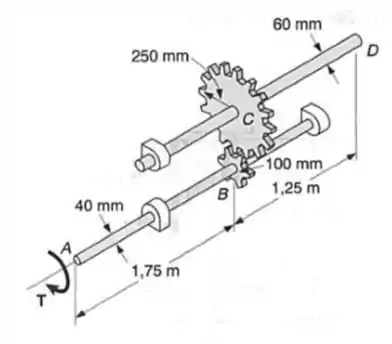
Dois eixos de aço são acoplados pelas engrenagens mostradas. Determinar a máxima tensão de cisalhamento em cada eixo, quando um torque T de 600   N ⋅ m é aplicado em A .

Passo 1

Este exercício é muito comum com problemas de torção e nos pede a tensão de cisalhamento máxima de cada eixo, que é obtida através da fórmula:

τ = T ⋅ c J

Onde:

  • τ Representa a tensão de cisalhamento.
  • T A torção a qual a barra está submetida.
  • c A distância do centro ao ponto de aplicação.
  • J O momento de inércia polar.

Lembrando que o momento de inércia polar é calculado como:

J = π ⋅ c 4 2

Além disso é importante lembrar que nas engrenagens a força entre elas é a mesma, logo o torque será diferente, lembrando que:

T = F ⋅ d

No caso das engrenages a distância d será equivalente ao raio. Como temos que as forças será iguais, podemos mudar essa equação para se tornar um pouco mais prática:

F = T d

Ou

F = T R

Como as forças são iguais, vamos ter que

F 1 = F 2

T 1 R ! = T 2 R 2

Passo 2

Vamos começar calculando os momentos de inércia polar para as barras A B e C D , para depois calcularmos o torque:

J = π ⋅ c 4 2

Para a barra A B , que tem diâmetro de 4 0   m m e raio de 20 m m

J = π ⋅ ( 20 × 10 - 3 ) 4 2

J = π ⋅ 160000 × 10 - 12 2

J = 251327 × 10 - 12   m 4

Para a barra C D , que tem diâmetro de 6 0   m m e raio de 30 m m

J = π ⋅ ( 30 × 10 - 3 ) 4 2

J = π ⋅ 810000 × 10 - 12 2

J = 1272345 × 10 - 12   m 4

Passo 3

Agora para calcular a tensão máxima nós precisamos do torque. Nós já possuímos o torque aplicado no eixo A B que é de 600   N ⋅ m mas precisamos saber qual será o torque desenvolvido no eixo C D para isso vamos utilizar a seguinte equação demonstrada no passo 1:

T 1 R ! = T 2 R 2

Logo vamos ter

T C D 250 = T A B 100

T C D 250 = 600 100

T C D = 250 ⋅ 600 100

T C D = 1500   N ⋅ m

Passo 4

Agora podemos calcular a tensão de cisalhamento para ambas as barras:

τ = T ⋅ c J

Primeiro para a barra A B , lembrando que ela tem raio igual a 20   m m

τ = 600 ⋅ 20 × 10 - 3 251327 × 10 - 12

τ = 600 ⋅ 2 0 251327 ⋅ ( 10 - 3 ) 10 - 12

τ = 0,0 477 × 10 9   P a

τ = 47,7 × 10 6   P a

τ = 47,7   M P a

Agora para a barra C D , lembrando que ela tem raio igual a 30   m m

τ = 1500 ⋅ 30 × 10 - 3 1272345 × 10 - 12

τ = 1500 ⋅ 30 1272345 ⋅ ( 10 - 3 ) 10 - 12

τ = 0,0354 × 10 9   P a

τ = 35,4 × 10 6   P a

τ = 35,4   M P a

logo a máxima tensão de cisalhamento em cada eixo será de

τ C D = 35,4     M P a

τ A B = 47,7   M P a

Resposta

τ C D = 35,4     M P a

τ A B = 47,7   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A seção transversal cheia mostrada na figura é feita de latão para o qual a tensão de cisalhamento admissível é de 55 MPa. Desprezando o efeito das concentrações de tensão, determine os menores diâmet
A haste sólida AB tem um diâmetro d A B = 60m m e é feita de aço para o qual a tensão de cisalhamento admissível é de 85 MPa. O tubo CD, que tem o diÂmetro externo de 90 mm e espessura de parede de 6
Resolva o problema 3.17 considerando que a direção de T c seja invertida.PROBLEMA 3.17 O eixo sólido mostrado é formado por um latão para cuja tensão de cisalhamento admissível é de 55 MPa. Negligenci
Um torque de T = 1000 N/m é aplicado de D, como mostra a figura. Sabendo que diâmetro do eixo AB é de 56 mm e que diâmetro do eixo CD é de 42 mm, determine a tensão de cisalhamento máxima no(a)eixo AB
A haste sólida AB tem um diâmetro dAB = 60 mm. O tubo CB tem um diâmetro externo de 90 mm e parede com 6 mm de espessura. Sabendo que ambos a haste e o tubo são feitos de aço e para o qual a tensão de