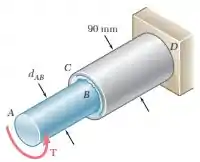
A haste sólida AB tem um diâmetro dAB = 60 mm. O tubo CB tem um diâmetro externo de 90 mm e parede com 6 mm de espessura. Sabendo que ambos a haste e o tubo são feitos de aço e para o qual a tensão de cisalhamento admissível é 75 MPa, determine o maior torque que pode ser aplicado em A.

Pessoal, a parada dessa questão é a seguinte, se a gente fizer a conta pra haste e pro tubo, a gente vai achar valores diferentes pro torque máximo. Isso porque são corpos diferentes e suportam esforços diferentes. Mas a nossa resposta vai ser o menor valor entre eles, porque, para que a estrutura como um todo aguente esse torque, cada uma das partes precisa suporta.

A expressão que relaciona as variáveis que a gente tem e que a gente quer é essa aqui, que dá o torque T em função do momento de inércia, da tensão de cisalhamento e do raio c do tubo.

Para a haste sólida:

Para o tubo, que é um cilindro oco, o momento de inercia é:

E, como queremos saber o torque máximo, a tensão de cisalhamento vai ser a tensão a tensão admissível:

Então agora é só a gente fazer os cálculos!